
(本小题满分13分)
如图,四边形 为矩形,
为矩形, 平面
平面 ,
, 为
为 上的点,且
上的点,且 平面
平面 .
.
(1)求证: ;
;
(2)求三棱锥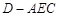 的体积;
的体积;
(3)设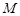 在线段
在线段 上,且满足
上,且满足 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得 平面
平面 .
.
(1)根据线面垂直的性质定理来证明线线垂直,同时能根据∴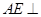 平面
平面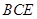 ,得到结论是关键的一步。
,得到结论是关键的一步。
(2)
(3) 点为线段
点为线段 上靠近
上靠近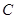 点的一个三等分点
点的一个三等分点
解析试题分析:
证明:(1)∵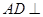 平面
平面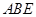 ,且
,且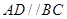
∴ 平面
平面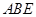 ,则
,则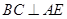 .………………………………………2分
.………………………………………2分
又∵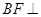 平面
平面 ,则
,则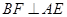 ,且
,且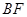 与
与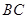 交于
交于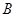 点,
点,
∴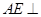 平面
平面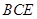 ,又
,又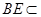 平面
平面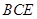 ∴
∴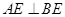 .………………4分
.………………4分
(2)由第(1)问得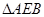 为等腰直角三角形,易求得
为等腰直角三角形,易求得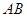 边上的高为
边上的高为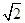 ,
,
∴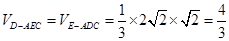 .…………………………………………………7分
.…………………………………………………7分
(3)在三角形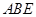 中过
中过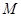 点作
点作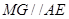 交
交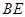 于
于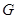 点,在三角形
点,在三角形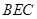 中过
中过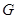 点作
点作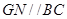 交
交 于
于 点,连
点,连 .
.
由比例关系易得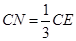 .………………………………………………………………9分
.………………………………………………………………9分
∵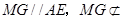 平面
平面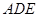 ,
,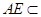 平面
平面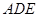 ,
,
∴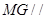 平面
平面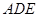 . 同理,
. 同理,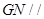 平面
平面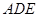 ,且
,且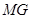 与
与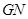 交于
交于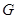 点,
点,
∴平面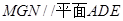 .………………………………………………………………11分
.………………………………………………………………11分
又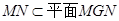 , ∴
, ∴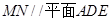 .
.
∴ 点为线段
点为线段 上靠近
上靠近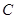 点的一个三等分点.…………………………………………13分
点的一个三等分点.…………………………………………13分
考点:线线的垂直证明,以及体积计算。
点评:解决该试题的关键是能利用线面垂直的性质定理来灵活的证明线线垂直,同时能根据等体积法求解体积,是常用的求解方法,属于基础题。


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.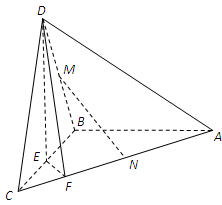
(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个多面体的直观图和三视图如图所示,其中 、
、 分别是
分别是 、
、 的中点,
的中点, 是
是 上的一动点,主视图与俯视图都为正方形。
上的一动点,主视图与俯视图都为正方形。

⑴求证: ;
;
⑵当 时,在棱
时,在棱 上确定一点
上确定一点 ,使得
,使得 ∥平面
∥平面 ,并给出证明。
,并给出证明。
⑶求二面角 的平面角余弦值。
的平面角余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
如图1,在等腰梯形 中,
中, ,
, ,
, ,
, 为
为 上一点,
上一点,  ,且
,且 .将梯形
.将梯形 沿
沿 折成直二面角
折成直二面角 ,如图2所示.
,如图2所示.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)设点 关于点
关于点 的对称点为
的对称点为 ,点
,点 在
在 所在平面内,且直线
所在平面内,且直线 与平面
与平面 所成的角为
所成的角为 ,试求出点
,试求出点 到点
到点 的最短距离.
的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com