
【题目】如表提供了甲产品的产量x(吨)与利润y(万元)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)计算相关指数R2的值,并判断线性模型拟合的效果.
参考公式: ![]() =
= 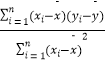 =
= 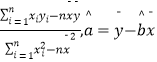 ,R2=1﹣
,R2=1﹣ 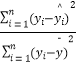 .
.
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,
且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1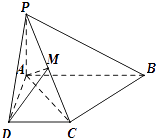
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合A={x|kx2﹣2x﹣1=0}只有一个元素,则实数k的取值集合为( )
A.{﹣1}
B.{0}
C.{﹣1,0}
D.(﹣∞,﹣1]∪{0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有f[f(x)﹣ ![]() ]=2,则f(2016)=( )
]=2,则f(2016)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设[x]表示不超过x的最大整数,如[1]=1,[0.5]=0,已知函数f(x)= ![]() ﹣k(x>0),若方程f(x)=0有且仅有3个实根,则实数k的取值范围是( )
﹣k(x>0),若方程f(x)=0有且仅有3个实根,则实数k的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数g(x)=mx2﹣2mx+n+1(m>0)在区间[0,3]上有最大值4,最小值0.
(1)求函数g(x)的解析式;
(2)设f(x)= ![]() .若f(2x)﹣k2x≤0在x∈[﹣3,3]时恒成立,求k的取值范围.
.若f(2x)﹣k2x≤0在x∈[﹣3,3]时恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com