
【题目】已知双曲线![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,直线
,直线![]() 与双曲线交于
与双曲线交于![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 的轨迹与矩形
的轨迹与矩形![]() 的四条边都相切,探究矩形
的四条边都相切,探究矩形![]() 对角线长是否为定值,若是,求出此值;若不是,说明理由.
对角线长是否为定值,若是,求出此值;若不是,说明理由.

【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)利用交轨法,求出点![]() 的轨迹方程;(2) 设点
的轨迹方程;(2) 设点![]() ,过点
,过点![]() 作椭圆的切线,则切线的斜率存在且不为0,设斜率为
作椭圆的切线,则切线的斜率存在且不为0,设斜率为![]() ,则切线方程为
,则切线方程为![]() ,
,
代入到椭圆方程整理,得![]() .由
.由![]() 得到
得到
![]() ,这个关于
,这个关于![]() 的一元二次方程的两根即为
的一元二次方程的两根即为![]() 与
与![]() ,
,
由![]() ,可知
,可知![]() ,即
,即![]() ,即点
,即点![]() 为矩形
为矩形![]() 外接圆的圆心,其中
外接圆的圆心,其中![]() 为直径,大小为
为直径,大小为![]() ,故矩形
,故矩形![]() 对角线长为定值
对角线长为定值![]() .
.
试题解析:
(1)设点![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
由题意,得![]() ,
, ![]() .
.
由![]() ,①
,①
![]() ,②
,②
两式相乘得![]() .
.
∵![]() ,
,
∴![]() ,
,
代入上式得
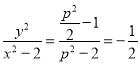
![]() ,
,
由①与![]() ,得
,得![]() ,
,
①÷②,得![]() .
.
故点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)设点![]() ,过点
,过点![]() 作椭圆的切线,
作椭圆的切线,
则切线的斜率存在且不为0,设斜率为![]() ,
,
则切线方程为![]() ,
,
代入到椭圆方程整理,
得![]() .
.
![]()
![]() ,
,
即![]() .
.
这个关于![]() 的一元二次方程的两根即为
的一元二次方程的两根即为![]() 与
与![]() ,
,
由![]() ,
,
得![]() .
.
设![]() 为坐标原点,故可知
为坐标原点,故可知![]() ,
,
同理,得![]() ,
,
即点![]() 为矩形
为矩形![]() 外接圆的圆心,其中
外接圆的圆心,其中![]() 为直径,大小为
为直径,大小为![]() ,
,
故矩形![]() 对角线长为定值
对角线长为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角![]() 和以
和以![]() 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点![]() 为半圈上一点(异于
为半圈上一点(异于![]() ,
,![]() ),点
),点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,
,![]() ,设
,设![]() .
.

(1)为了使工艺礼品达到最佳观赏效果,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,工艺礼品达到最佳观赏效果;
为何值时,工艺礼品达到最佳观赏效果;
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,
为何值时,![]() 取得最大值,并求该最大值.
取得最大值,并求该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱
B. 四棱锥的四个侧面都可以是直角三角形
C. 有两个平面互相平行,其余各面都是梯形的多面体是棱台
D. 棱台的各侧棱延长后不一定交于一点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=
,AB=BC=![]() AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到如图2中△A1BE的位置,得到四棱锥A1-BCDE.
AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到如图2中△A1BE的位置,得到四棱锥A1-BCDE.
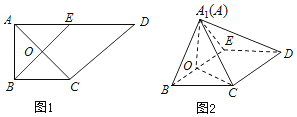
(Ⅰ)证明:CD⊥平面A1OC;
(Ⅱ)当平面A1BE⊥平面BCDE时,四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】母线长为![]() ,底面半径为
,底面半径为![]() 的圆锥内有一球
的圆锥内有一球![]() ,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球
,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球![]() 都相切,这样的小球最多可放入__________个.
都相切,这样的小球最多可放入__________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
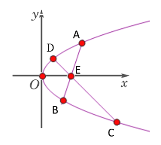
【题目】已知点![]() 为抛物线
为抛物线![]() 内一定点,过
内一定点,过![]() 作两条直线交抛物线于
作两条直线交抛物线于![]() ,且
,且![]() 分别是线段
分别是线段![]() 的中点.
的中点.
(1)当![]() 时,求△
时,求△![]() 的面积的最小值;
的面积的最小值;
(2)若![]() 且
且![]() ,证明:直线
,证明:直线![]() 过定点,并求定点坐标。
过定点,并求定点坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“既要金山银山,又要绿水青山”。某风景区在一个直径![]() 为
为![]() 米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点
米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点![]() (与
(与![]() 不重合),沿
不重合),沿![]() 修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧
修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧![]() 修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。
修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。

(1)设![]() (弧度),将绿化带的总长度表示为
(弧度),将绿化带的总长度表示为![]() 的函数
的函数![]() ;
;
(2)求绿化带的总长度![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且椭圆经过点
,且椭圆经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与圆
与圆![]() 相切:
相切:
(ⅰ)求圆![]() 的标准方程;
的标准方程;
(ⅱ)若直线![]() 过定点
过定点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() ,与圆
,与圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月10日,我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖,以青蒿素类药物为主的联合疗法已经成为世界卫生组织推荐的抗疟疾标准疗法,目前,国内青蒿人工种植发展迅速,调查表明,人工种植的青蒿的长势与海拨高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为![]() ,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标
,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标![]() 的值评定人工种植的青蒿的长势等级,若
的值评定人工种植的青蒿的长势等级,若![]() ,则长势为一级;若
,则长势为一级;若![]() ,则长势为二极;若
,则长势为二极;若![]() ,则长势为三级,为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果:
,则长势为三级,为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果:
种植地编号 |
|
|
|
|
|
|
|
|
|
|
|
种植地编号 |
|
|
|
|
|
|
|
|
|
|
|
(1)若该地有青蒿人工种植地180个,试估计该地中长势等级为三级的个数;
(2)从长势等级为一级的青蒿人工种植地中随机抽取两个,求这两个人工种植地的综合指标![]() 均为4个概率.
均为4个概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com