
���� ��1����P��x0��y0������Q��-x0��-y0����$\overrightarrow{MP}$=$��{x}_{0}��{y}_{0}-\frac{1}{2}��$��$\overrightarrow{MQ}$=$��-{x}_{0}��-{y}_{0}-\frac{1}{2}��$�������������������ʼ���${y}_{0}^{2}$=1-$\frac{{x}_{0}^{2}}{9}$����${x}_{0}^{2}$��[0��9]�����ɵó���
��2����P����ԲC���ڵ�һ�����ڵĵ㣬��l��б��k�ʣ�0��+�ޣ�����l��y=kx����k��$��0��\frac{1}{2}]$ʱ����DFM��ֱ��l���õ��߶ε������˵�ֱ���ֱ��l��y=kx��ֱ��DM��EM�Ľ���ΪA��B������֪DM��y=x+$\frac{1}{2}$��EM��y=-x+$\frac{1}{2}$������������ɵ�ֱ�ߵĽ��㣬��������֮��ľ��빫ʽ���ɵó���
��� �⣺��1����P��x0��y0������Q��-x0��-y0����$\overrightarrow{MP}$=$��{x}_{0}��{y}_{0}-\frac{1}{2}��$��$\overrightarrow{MQ}$=$��-{x}_{0}��-{y}_{0}-\frac{1}{2}��$��
���=$\overrightarrow{MP}$•$\overrightarrow{MQ}$=$-{x}_{0}^{2}$-${y}_{0}^{2}$+$\frac{1}{4}$����${y}_{0}^{2}$=1-$\frac{{x}_{0}^{2}}{9}$��
��$��=-\frac{8{x}_{0}^{2}}{9}$-$\frac{3}{4}$����${x}_{0}^{2}$��[0��9]����ˡ�$[-\frac{35}{4}��-\frac{3}{4}]$��
��2����P����ԲC���ڵ�һ�����ڵĵ㣬��l��б��k�ʣ�0��+�ޣ�����l��y=kx��
��k��$��0��\frac{1}{2}]$ʱ����DFM��ֱ��l���õ��߶ε������˵�ֱ���ֱ��l��y=kx��ֱ��DM��EM�Ľ���ΪA��B������֪DM��y=x+$\frac{1}{2}$��EM��y=-x+$\frac{1}{2}$��
����$\left\{\begin{array}{l}{y=kx}\\{y=x+\frac{1}{2}}\end{array}\right.$�����A$��\frac{1}{2��k-1��}��\frac{k}{2��k-1��}��$��
����$\left\{\begin{array}{l}{y=kx}\\{y=-x+\frac{1}{2}}\end{array}\right.$�����B$��\frac{1}{2��k+1��}��\frac{k}{2��k+1��}��$��
����s=|AB|=$\sqrt{{k}^{2}+1}$|xA-xB|=$\sqrt{{k}^{2}+1}$•$\frac{1}{1-{k}^{2}}$��
��k��$��\frac{1}{2}��+�ޣ�$ʱ����DEM��ֱ��l���õ��߶ε������˵�ֱ���ֱ��l��y=kx��ֱ��DE��EM�Ľ���G��B������֪DE��y=-$\frac{1}{2}$��
����$\left\{\begin{array}{l}{y=kx}\\{y=-\frac{1}{2}}\end{array}\right.$�����G$��-\frac{1}{2k}��-\frac{1}{2}��$��
����s=s��k��=|GB|=$\sqrt{{k}^{2}+1}$$•\frac{2k+1}{2k��k+1��}$��
����������s=$\left\{\begin{array}{l}{\sqrt{{k}^{2}+1}•\frac{1}{1-{k}^{2}}��k�ʣ�0��\frac{1}{2}]}\\{\sqrt{{k}^{2}+1}•\frac{2k+1}{2k��k+1��}��k�ʣ�\frac{1}{2}��+�ޣ�}\end{array}\right.$��
���� ���⿼������Բ�ı����̼������ʡ���������ֱ�ߵĽ��㡢����֮��ľ��빫ʽ���������������ʣ���������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��c | B�� | a��c���� | ||
| C�� | a��c�����ƽ�л��ཻ | D�� | a��c�ཻ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 21 | B�� | 9 | C�� | 5 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $3+2\sqrt{2}$ | B�� | $4\sqrt{2}$ | C�� | 4+2$\sqrt{3}$ | D�� | $4\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
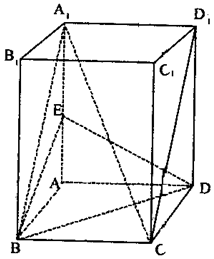 ��ͼ���ڳ�����ABCD-A1B1C1D1�У���AD=DC=3��DD1=4��E��A1A���е㣮
��ͼ���ڳ�����ABCD-A1B1C1D1�У���AD=DC=3��DD1=4��E��A1A���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com