
【题目】已知方程![]() 有4个不同的根,则实数
有4个不同的根,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由![]() ,得
,得![]() ,设
,设![]() ,对函数
,对函数![]() 求导分析其单调性和图象趋势,作出大致图象,根据数形结合可得实数
求导分析其单调性和图象趋势,作出大致图象,根据数形结合可得实数![]() 的取值范围.
的取值范围.
方法一:易知![]() 是方程
是方程![]() 的一个根,显然
的一个根,显然![]() ,当
,当![]() 且
且![]() 时,由
时,由![]() ,
,
得![]() ,设
,设![]() ,则
,则![]() 的图象与直线
的图象与直线![]() 有3个不同的交点.
有3个不同的交点.
当![]() 时,
时,![]() ,因为
,因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]() 。
。
当![]() 且
且![]() 时,
时,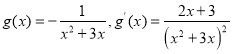 ,
,
令![]() 得
得![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
所以函数![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增,且
上单调递增,且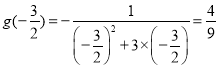 ,
,
且当x从左边趋近于0和从右边趋近于-3时,![]() ,当x从左边趋近于-3时,
,当x从左边趋近于-3时,![]() ,当
,当![]() 时,
时,![]() ,
,
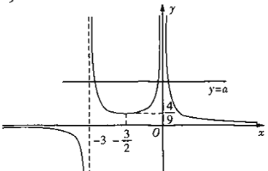
作出函数![]() 的大致图象如下图所示,由图可知,
的大致图象如下图所示,由图可知,![]() ,
,
综上,实数a的取值范围是![]() ,
,
故选:A。
方法二:易知![]() 是方程
是方程![]() 的一个根,当
的一个根,当![]() 时,由
时,由![]() ,得
,得![]() ,
,
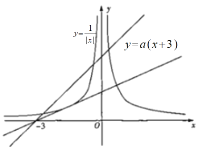
则该方程有3个不同的根,在同一坐标系内作出函数![]() 和
和![]() 的图象,如下图所示:
的图象,如下图所示:
当![]() 时,当
时,当![]() 与曲线
与曲线 ![]() 的左支相切时,由
的左支相切时,由![]() 得
得![]() 得
得![]() ,由图可知,当
,由图可知,当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 有3个不同的交点,即方程
有3个不同的交点,即方程![]() 有3个不同的根,
有3个不同的根,
综上,实数a的取值范围是![]() ,
,
故选:A.


科目:高中数学 来源: 题型:
【题目】为改善环境,节约资源,我国自2019年起在全国地级及以上城市全面启动生活垃圾分类,垃圾分类已成为一种潮流.某市一小区的主管部门为了解居民对垃圾分类的认知是否与其受教育程度有关,对该小区居民进行了随机抽样调查,得到如下统计数据的列联表:
知道如何对垃圾进行分类 | 不知道如何对垃圾进行分类 | 合计 | |
未受过高等教育 |
| 10 |
|
受过高等教育 |
|
|
|
合计 |
|
| 50 |
(1)求列联表中的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率;
的值,并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率;
(2)根据列联表判断能否有![]() 的把握认为该小区居民对垃圾分类的认知与其受教育程度有关?
的把握认为该小区居民对垃圾分类的认知与其受教育程度有关?
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
|
|
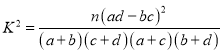 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①
,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①![]() ;②
;②![]() ;③
;③![]() .
.
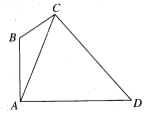
(1)求![]() 的大小;
的大小;
(2)求△ADC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lnx,g(x)=ex.
(1)若函数φ (x) = f (x)-![]() ,求函数φ (x)的单调增区间;
,求函数φ (x)的单调增区间;
(2)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com