
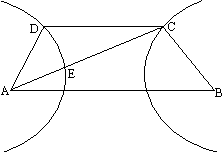
如下图所示,已知梯形ABCD中,|AB|=2|CD|,点E分有向线![]() 所成的比为λ,双曲线过C、D、E三点,且以A、B为焦点.当
所成的比为λ,双曲线过C、D、E三点,且以A、B为焦点.当![]() ≤λ≤
≤λ≤![]() 时,求双曲线离心率e的取值范围.
时,求双曲线离心率e的取值范围.
|
解析:以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xOy,则CD⊥y轴.因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称. 依题意,记A(-c,0),C( 由定比分点坐标公式得x0= 设双曲线的方程为 由点C、E在双曲线上,将点C、E的坐标和e=
由①式得 将③式代入②式,整理得 由题设 解得 所以双曲线的离心率e的取值范围为[ 点评:本题主要考查坐标法、定比分点坐标公式、双曲线的概念和性质以及推理、运算能力和综合应用数学知识解决问题的能力. |


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:


查看答案和解析>>
科目:高中数学 来源: 题型:
| BP | PC |

查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
如下图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC, ,PA⊥底面ABCD,且
,PA⊥底面ABCD,且 ,M是PB的中点.
,M是PB的中点.

(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角的余弦值;
(3)求面AMC与面BMC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:044
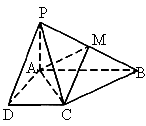
如下图所示,已知四棱锥
P-ABCD的底面为直角梯形,AB∥DC,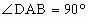 ,PA⊥底面ABCD,且
,PA⊥底面ABCD,且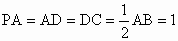 ,M是PB的中点.
,M是PB的中点.
(1)
证明:面PAD⊥面PCD;(2)
求AC与PB所成的角的余弦值;(3)
求面AMC与面BMC所成二面角的余弦值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com