
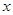 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与
(亿千瓦时)与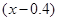 元成反比例.又当
元成反比例.又当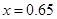 时,
时,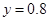 .
. 与
与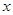 之间的函数关系式;
之间的函数关系式;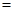 用电量
用电量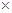 (实际电价-成本价)]
(实际电价-成本价)] 与
与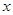 之间的函数关系式为
之间的函数关系式为 (
( );(2)当电价调至
);(2)当电价调至 元时,本年度电力部门的收益将比上年度增加20%.
元时,本年度电力部门的收益将比上年度增加20%.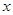 ,并与实际定义域对照,作出取舍,实际应用题对题意的理解能力要求比较高,一定要仔细读题和审题.
,并与实际定义域对照,作出取舍,实际应用题对题意的理解能力要求比较高,一定要仔细读题和审题. 与
与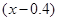 成反比例,所以设
成反比例,所以设 (
( ) 3分
) 3分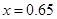 ,
,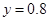 代入上式,得
代入上式,得 ,即有
,即有 5分
5分 , 6分
, 6分 与
与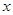 之间的函数关系式为
之间的函数关系式为 (
( ). 7分
). 7分 11分
11分 ,解得
,解得 ,
, .
. ,
, 都是所列方程的根.但因为
都是所列方程的根.但因为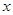 的取值范围是0.55~0.75,
的取值范围是0.55~0.75, 不符合题意,应舍去.所以
不符合题意,应舍去.所以 . 13分
. 13分 元时,本年度电力部门的收益将比上年度增加20%. 14分
元时,本年度电力部门的收益将比上年度增加20%. 14分

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源:不详 题型:解答题
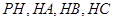 构成,其底端三点
构成,其底端三点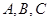 均匀地固定在半径为
均匀地固定在半径为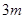 的圆
的圆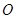 上(圆
上(圆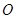 在地面上),
在地面上),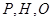 三点相异且共线,
三点相异且共线,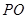 与地面垂直. 现要求点
与地面垂直. 现要求点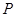 到地面的距离恰为
到地面的距离恰为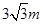 ,记用料总长为
,记用料总长为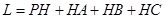 ,设
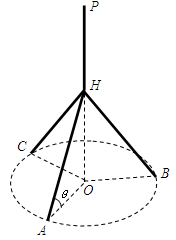
,设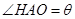 .
.
 表示为
表示为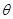 的函数,并注明定义域;
的函数,并注明定义域;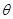 的正弦值是多少时,用料最省?
的正弦值是多少时,用料最省?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.¬p:?x∈R,cosx≤1 | B.¬p:?x∈R,cosx≤1 |
| C.¬p:?x∈R,cosx<1 | D.¬p:?x∈R,cosx<1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. f:x→y=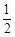 x x | B. f:x→y=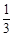 x x | C. f:x→y=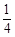 x x | D. f:x→y=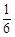 x x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
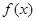 的定义域为
的定义域为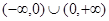 ,
,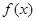 是奇函数,且当
是奇函数,且当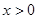 时,
时,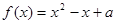 ,若函数
,若函数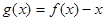 的零点恰有两个,则实数
的零点恰有两个,则实数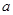 的取值范围是( )
的取值范围是( )A.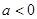 | B.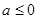 |
C.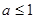 | D.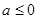 或 或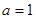 |
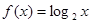 在其定义域内任意的
在其定义域内任意的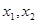 且
且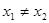 ,有如下结论:
,有如下结论: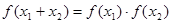 ;
;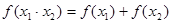 ;
;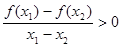 ;
;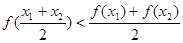 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com