
【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
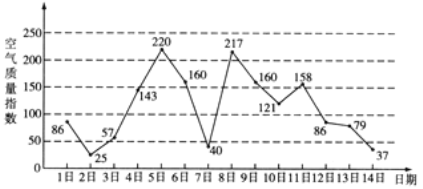
(1)求此人到达当日空气重度污染的概率;
(2)求此人在该市停留期间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
【答案】(1)![]() (2)
(2)![]() (3)从3月5日开始连续三天的空气质量指数方差最大
(3)从3月5日开始连续三天的空气质量指数方差最大
【解析】
(1)直接利用古典概型的概率公式求解;
(2)事件“此人在该市停留期间只有1天空气重度污染”等价于“此人到达该市的日期是4日或5日或7日或8日”,再利用古典概型的概率得解;
(3)由图观察得从3月5日开始连续三天的空气质量指数方差最大.
解:(1)在3月1日至3月13日这13天中,5日、8日共2天的空气重试污染,所以此人到达当日空气重度污染的概率为![]() .
.
(2)根据题意,事件“此人在该市停留期间只有1天空气重度污染”等价于“此人到达该市的日期是4日或5日或7日或8日”,所以此人在该市停留期间只有1天空气重度污染的概率为![]() .
.
(3)由图可以看出,从3月5日开始连续三天的空气质量指数方差最大.


科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
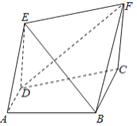
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,政府相关部门引导乡村发展旅游的同时,鼓励农户建设温室大棚种植高品质农作物.为了解某农作物的大棚种植面积对种植管理成本的影响,甲,乙两同学一起收集6家农户的数据,进行回归分折,得到两个回归摸型:模型①:![]() ,模型②:
,模型②: ![]() ,对以上两个回归方程进行残差分析,得到下表:
,对以上两个回归方程进行残差分析,得到下表:
种植面积 | 2 | 3 | 4 | 5 | 7 | 9 | |
每亩种植管理成本 | 25 | 24 | 21 | 22 | 16 | 14 | |
模型① | 估计值 | 25.27 | 23.62 | 21.97 | 17.02 | 13.72 | |
残差 | -0.27 | 0.38 | -0.97 | -1.02 | 0.28 | ||
模型② |
| 26.84 | 20.17 | 18.83 | 17.31 | 16.46 | |
| -1.84 | 0.83 | 3.17 | -1.31 | -2.46 | ||
(1)将以上表格补充完整,并根据残差平方和判断哪个模型拟合效果更好;
(2)视残差![]() 的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
附: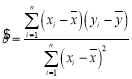 ,
,![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,我国老年人口比例不断上升,造成日趋严峻的人口老龄化问题.2019年10月12日,北京市老龄办、市老龄协会联合北京师范大学中国公益研究院发布《北京市老龄事业发展报告(2018)》,相关数据有如下图表.规定年龄在15岁至59岁为“劳动年龄”,具备劳动力,60岁及以上年龄为“老年人”,据统计,2018年底北京市每2.4名劳动力抚养1名老年人.
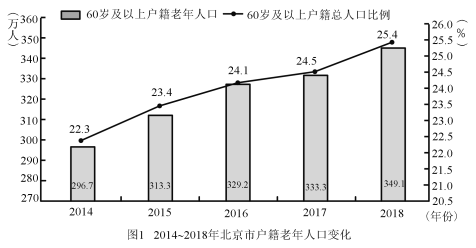
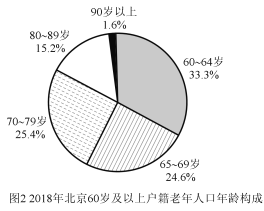
(Ⅰ)请根据上述图表计算北京市2018年户籍总人口数和北京市2018年的劳动力数;(保留两位小数)
(Ⅱ)从2014年起,北京市老龄人口与年份呈线性关系,比照2018年户籍老年人人口年龄构成,预计到2020年年底,北京市90以上老人达到多少人?(精确到1人)
(附:对于一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: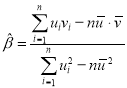 ,
,![]() .
.![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )

A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图被称为“中华第一图”,闪烁着中华文明进程的光辉,它是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”,设圆O:![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )

A.函数![]() 是圆O的一个太极函数
是圆O的一个太极函数
B.圆O的所有非常数函数的太极函数都不能为偶函数
C.函数![]() 是圆O的一个太极函数
是圆O的一个太极函数
D.函数![]() 的图象关于原点对称是
的图象关于原点对称是![]() 为圆O的太极函数的充要条件
为圆O的太极函数的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥C﹣ABNM中,四边形ABNM的边长均为2,△ABC为正三角形,MB![]() ,MB⊥NC,E,F分别为MN,AC中点.
,MB⊥NC,E,F分别为MN,AC中点.
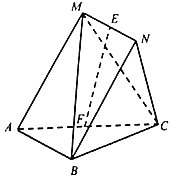
(Ⅰ)证明:MB⊥AC;
(Ⅱ)求直线EF与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
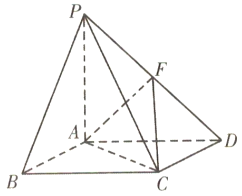
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com