练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】现将“□”和“○”按照如下规律从左到右进行排列：若每一个“□”或“○”占1个位置，即上述图形中，第1位是“□”，第4位是“○”，第7位是 “□”，则在第2017位之前（不含第2017位），“○”的个数为（ ）

    □,○,□,○,○,○,□,○,○,○,○,○,□,○,○,○,○,○,○,○

    A.1970B.1971C.1972D.1973

    【答案】B

    【解析】

    根据题意，以“□,○”为第1组，“□,○,○,○,”为第2组，如此类推，发现规律，将问题转化为计算等差数列前项和，即可求得结果.

    记“□,○”为第1组，“□,○,○,○,”为第2组，“□,○,○,○,○,○”为第3组，

    以此类推，可知第k组共有2k个图形，

    故前k组共有个图形，

    因为，

    所以在前2016位中共有45个“□”，

    从而可知有201645=1971个“○”.

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】从编号为1，2，3，4，…，10的10个大小、形状相同的小球中，任取5个球.如果某两个球的编号相邻，则称这两个球为一组“好球”.

    （1）求任取的5个球中至少有一组“好球”的概率；

    （2）在任取的5个球中，记“好球”的组数为X，求随机变量Ｘ的概率分布列和均值E(X).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是等比数列的公比大于，其前项和为，是等差数列，已知，，，.

    （1）求，的通项公式

    （2）设，数列的前项和为，求；

    （3）设，其中,求

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面是菱形，底面，分别是的中点，，，.

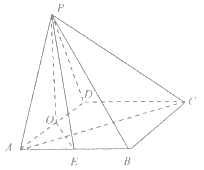
    （I）证明：；

    （II）求直线与平面所成角的正弦值；

    （III）在边上是否存在点，使与所成角的余弦值为，若存在，确定点位置；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于集合，，，，定义.

    集合中的元素个数记为，当，称集合具有性质.

    （1）已知集合，，写出，的值，并判断集合是否具有性质；

    （2）设集合具有性质，判断集合中的三个元素是否能组成等差数列，请说明理由；

    （3）若数列是以为首项，2为公比的等比数列. 数列中的前100项：组成的集合记作，将集合中的所有元素从小到大排序，即满足，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平行六面体中，，，.

    （1）证明：.

    （2）若平面平面，且，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，矩形中， ， ，点是上的动点．现将矩形沿着对角线折成二面角，使得．

    （Ⅰ）求证：当时， ；

    （Ⅱ）试求的长，使得二面角的大小为．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C1的参数方程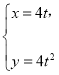（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C2的极坐标方程为ρ＝4sinθ．

    （1）求C1的极坐标方程与C2的直角坐标方程；

    （2）已知射线与C1交于O，P两点，与C2交于O，Q两点，且Q为OP的中点，求α．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如城某观光区的平面示意图如图所示，其中矩形的长千米，宽千米，半圆的圆心为中点.为了便于游客观光休闲，在观光区铺设一条由圆弧、线段、组成的观光道路.其中线段经过圆心，且点在线段上（不含线段端点、）.已知道路、的造价为元每千米，道路造价为元每千米，设，观光道路的总造价为.

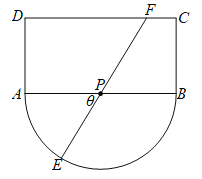
    （1）试求与的函数关系式：；

    （2）当为何值时，观光道路的总造价最小.

    查看答案和解析>>

    同步练习册答案