
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,总有
时,总有![]() ,求
,求![]() 的最小值;
的最小值;
(2)对于![]() 中任意
中任意![]() 恒有
恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果对任意n∈N*,都有bn+![]() t≤t2,求实数t的取值范围.
t≤t2,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有且仅有2个零点,对于下列4个结论:①在区间
上有且仅有2个零点,对于下列4个结论:①在区间![]() 上存在
上存在![]() ,满足
,满足![]() ;②
;②![]() 在区间
在区间![]() 有且仅有1个最大值点;③
有且仅有1个最大值点;③![]() 在区间
在区间![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() ,其中所有正确结论的编号是( )
,其中所有正确结论的编号是( )
A.①③B.①③④C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x),x∈[1,+∞),数列{an}满足![]() ,
,
①函数f(x)是增函数;
②数列{an}是递增数列.
写出一个满足①的函数f(x)的解析式______.
写出一个满足②但不满足①的函数f(x)的解析式______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() :
: ![]() 满足:
满足: ![]() .记
.记![]() 的前
的前![]() 项和为
项和为![]() ,并规定
,并规定![]() .定义集合
.定义集合![]() ,
, ![]()
![]() ,
, ![]() .
.
(Ⅰ)对数列![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求集合
,求集合![]() ;
;
(Ⅱ)若集合![]() ,
, ![]() ,证明:
,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .对所有满足
.对所有满足![]() 的数列
的数列![]() ,求集合
,求集合![]() 的元素个数的最小值.
的元素个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明朝的程大位在《算法统宗》中(1592年),有这么个算法歌诀:三人同行七十稀,五树梅花廿一枝,七子团圆正半月,除百零五便得知.它的意思是说:求某个数(正整数)的最小正整数值,可以将某数除以3所得的余数乘以70,除以5所得的余数乘以21,除以7所得的余数乘以15,再将所得的三个积相加,并逐次减去105,减到差小于105为止,所得结果就是这个数的最小正整数值.《孙子算经》上有一道极其有名的“物不知数”问题:“今有物不知其数,三三数之余二,五五数之余三,七七数之余二,问物几何.”用上面的算法歌诀来算,该物品最少是几件( )
A.21B.22C.23D.24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“无桩有站”模式的公共自行车日益普及,即传统自行车加装智能锁,实现扫码租车及刷卡租车、某公司量产了甲、乙两种款式的公共自行车并投人使用,为了调查消费者对两种自行车的租赁情况,现随机抽取这两种款式的自行车各100辆,分别统计了每辆车在某周内的出租次数,得到甲、乙两种自行车这周内出租次数的频数分布表:
甲 | |||||
出租次数(单位:次) |
|
|
|
|
|
频数 | 10 | 10 | 60 | 15 | 5 |
乙 | |||||
出租次数(单位:次) |
|
|
|
|
|
频数 | 20 | 25 | 25 | 10 | 20 |
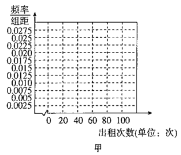
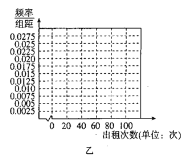
(1)根据频数分布表,完成上面频率分布直方图,并根据频率分布直方图比较甲、乙两种自行车这周内出租次数方差的大小(不必说明理由);
(2)如果两种自行车每次出租获得的利润相同,该公司决定大批量生产其中一种投入某城市使用,请你根据所学的统计知识,给出建议应该生产哪一种自行车,并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com