
【题目】关于函数的对称性有如下结论:对于给定的函数![]() ,如果对于任意的
,如果对于任意的![]() 都有
都有![]() 成立
成立![]() 为常数),则函数
为常数),则函数![]() 关于点
关于点![]() 对称.
对称.
(1)用题设中的结论证明:函数![]() 关于点
关于点![]() ;
;
(2)若函数![]() 既关于点
既关于点![]() 对称,又关于点
对称,又关于点![]() 对称,且当
对称,且当![]() 时,
时,![]() ,求:①
,求:①![]() 的值;
的值;
②当![]() 时,
时,![]() 的表达式.
的表达式.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根据题设中的结论证明即可;
(2)由题意可得![]() ,①代值计算即可;②由
,①代值计算即可;②由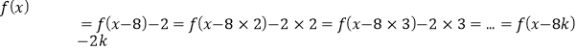 ,然后代值计算即可.
,然后代值计算即可.
(1)f(x)=![]() 的定义域为{x|x≠3},对任意x≠3有f(3﹣x)+f(3﹣x)=(﹣2﹣
的定义域为{x|x≠3},对任意x≠3有f(3﹣x)+f(3﹣x)=(﹣2﹣![]() )+(﹣2﹣
)+(﹣2﹣![]() )=﹣4,
)=﹣4,
∴函数f(x)=![]() 关于点(3,﹣2)对称;
关于点(3,﹣2)对称;
(2)函数f(x)关于点(2,0)对称,
∴f(2+x)+f(2﹣x)=0,
即f(x)+f(4﹣x)=0,
又关于点(﹣2,1)对称,
∴f(﹣2+x)+f(﹣2﹣x)=2,
即f(x)+f(﹣4﹣x)=2,
∴f(﹣4﹣x)=2+f(4﹣x),
即f(x+8)=f(x)﹣2,
①f(﹣5)=f(3)+2=23+3×3+2=19,
②x∈(8k﹣2,8k+2),x﹣8k∈(﹣2,2),4﹣(x﹣8k)∈(2,6),
∴f(x)=f(x﹣8)﹣2=f(x﹣8×2)﹣2×2=f(x﹣8×3)﹣2×3=…=f(x﹣8k)﹣2k,
又由f(t)=﹣f(4﹣t),
∴f(x)=f(x﹣8k)﹣2k=﹣f[4﹣(x﹣8k)]﹣2k=﹣[24﹣(x﹣8k)+3(4﹣(x﹣8k))]﹣2k,
∴即当x∈(8k﹣2,8k+2),k∈Z时,f(x)=﹣24﹣x+8k+3x﹣26k﹣12.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】张明与张华两人做游戏,下列游戏中不公平的是( )
①抛掷一枚骰子,向上的点数为奇数则张明获胜,向上的点数为偶数则张华获胜;
②同时抛掷两枚硬币,恰有一枚正面向上则张明获胜,两枚都正面向上则张华获胜;
③从一副不含大小王的扑克牌中抽一张,扑克牌是红色的则张明获胜,扑克牌是黑色的则张华获胜;
④张明、张华两人各写一个数字6或8,如果两人写的数字相同张明获胜,否则张华获胜.
A. ①② B. ② C. ②③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为![]() ,且
,且![]() 、
、![]() .若
.若![]() ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.15),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65],并绘制出频率分布直方图,如图所示是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.

(1)求这次铅球投掷成绩合格的人数;
(2)你认为这次铅球投掷的同学的成绩的中位数在第几组?请说明理由;
(3)若参加这次铅球投掷的学生中,有5人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加相关部门组织的经验交流会,已知a、b 两位同学的成绩均为优秀,求a、b 两位同学中至少有1人被选到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax﹣1|
(1)若f(x)≤2的解集为[﹣3,1],求实数a的值;
(2)若a=1,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤3﹣2m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校夏令营有3名男同学![]() 和3名女同学
和3名女同学![]() ,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
一年级 | 二年级 | 三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
(1)用表中字母列举出所有可能的结果;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|.
(1)当a=2时,解不等式f(x)≥7﹣|x﹣1|;
(2)若f(x)≤1的解集为[0,2], ![]() =a(m>0,n>0),求证:m+4n≥2
=a(m>0,n>0),求证:m+4n≥2 ![]() +3.
+3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com