
【题目】已知函数![]() ,函数
,函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
【答案】见解析
【解析】(1)因为![]() ,则由题意知
,则由题意知![]() ,所以
,所以![]() ,即
,即![]() .………1分
.………1分
所以![]() ,定义域为
,定义域为![]() .
.
![]() .……………2分
.……………2分
当![]() 时,由
时,由![]() ,得函数
,得函数![]() 的递增区间为
的递增区间为![]() ,
,
由![]() ,得函数
,得函数![]() 的递减区间为
的递减区间为![]() ;……………4分
;……………4分
当![]() 时,由
时,由![]() ,得函数
,得函数![]() 的递增区间为
的递增区间为![]() ,……………5分
,……………5分
(2)令![]() ,则
,则![]() .
.
根据题意,当![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() .……………6分
.……………6分
①当![]() 时,
时,![]() ,
,![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符合题意. ……………7分
,所以不符合题意. ……………7分
②当![]() 时,
时,![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() 所以不符合题意. ……………9分
所以不符合题意. ……………9分
③当![]() 时,
时,![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是减函数,
上是减函数,
于是“![]() 对任意
对任意![]() 都成立”的充要条件是
都成立”的充要条件是![]() ,
,
即![]() ,解得
,解得![]() ,故取
,故取![]() ,……………11分
,……………11分
综上,![]() .……………12分
.……………12分
【命题意图】本题主要考查利用导数研究函数的单调性、函数与方程、不等式解法等基础知识,意在考查
逻辑推理能力、等价转化能力、运算求解能力,以及考查函数与方程思想、分类讨论思想.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某厂生产某种产品x(百台),总成本为C(x)(万元),其中固定成本为2万元,每生产1百台,成本增加1万元,销售收入 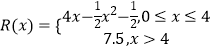 (万元),假定该产品产销平衡.
(万元),假定该产品产销平衡.
(1)若要该厂不亏本,产量x应控制在什么范围内?
(2)该厂年产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.据进一步测定,每毫升血液中含药量不少于0.25微克时,治疗疾病有效,则服药一次治疗该疾病有效的时间为( ) 
A.4小时
B.![]()
C.![]()
D.5小时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 ![]() ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(﹣1,1)上的函数f(x)满足:对任意x,y∈(﹣1,1)都有f(x)+f(y)=f(x+y).
(Ⅰ)求证:函数f(x)是奇函数;
(Ⅱ)如果当x∈(﹣1,0]时,有f(x)<0,试判断f(x)在(﹣1,1)上的单调性,并用定义证明你的判断;
(Ⅲ)在(Ⅱ)的条件下,若a﹣8x+1>0对满足不等式f(x﹣ ![]() )+f(
)+f( ![]() ﹣2x)<0的任意x恒成立,求a的取值范围.
﹣2x)<0的任意x恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,第一年投入资金1000万元,出售产品收入40万元,预计以后每年的投入资金是上一年的一半,出售产品所得收入比上一年多80万元,同时,当预计投入的资金低于20万元时,就按20万元投入,且当年出售产品收入与上一年相等.
(1)求第![]() 年的预计投入资金与出售产品的收入;
年的预计投入资金与出售产品的收入;
(2)预计从哪一年起该公司开始盈利?(注:盈利是指总收入大于总投入)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,分别根据下列条件解三角形,其中有两个解的是( )
A.a=7,b=14,A=30°
B.a=20,b=26,A=150°
C.a=30,b=40,A=30°
D.a=72,b=60,A=135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com