
【题目】已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=900,BC=2,AC=![]() ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C.
(Ⅰ)求侧棱A1A与底面ABC所成角的大小;
(Ⅱ)求侧面A1ABB1与底面ABC所成二面角的大小。

【答案】(1)见解析;(2)600
【解析】
(Ⅰ)作A1D⊥AC,垂足为D,由平面A1ACC1⊥平面ABC可得A1D⊥平面ABC,故∠A1AD即为A1A与平面ABC所成的角,解三角形可得∠A1AD=450即为所求.(Ⅱ)方法一:用几何法,作出两平面所成的二面角,解直角三角形可得所求角的大小.方法二:建立空间直角坐标系,求出两平面的法向量,借助两法向量夹角求出二面角的大小.
(Ⅰ)解:作A1D⊥AC,垂足为D,
∵平面A1ACC1⊥平面ABC,平面A1ACC1∩平面ABC![]() ,
,
∴A1D⊥平面ABC,
∴∠A1AD即为A1A与平面ABC所成的角.
∵AA1⊥A1C,AA1=A1C,
∴ ∠A1AD=450,
∴侧棱A1A与底面ABC所成角为450.
(Ⅱ)解法一:作DE⊥AB,垂足为E,连A1E,则有A1D⊥平面ABC,
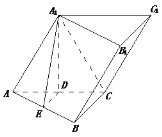
由三垂线定理得A1E⊥AB,
∴ ∠A1ED是平面A1ABB1与平面ABC所成二面角的平面角.
由已知得AB⊥BC,所以ED∥BC.
又D是AC的中点,BC=2,AC=![]() ,
,
∴ DE=1,AD=A1D=![]() ,
,
在![]()
∴∠A1ED=600,
∴侧面A1ABB1与底面ABC所成二面角的大小为600.
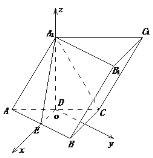
(Ⅱ)解法二:由(Ⅰ)可知![]() ⊥平面ABC,于是以
⊥平面ABC,于是以![]() 为原点,过点平行于BC、AB的直线为x、y轴,建立空间直角坐标系,如图所示.
为原点,过点平行于BC、AB的直线为x、y轴,建立空间直角坐标系,如图所示.
则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,得
,得![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() .
.
又平面ABC的法向量为![]() ,
,
∴ ,
,
由图形得侧面A1ABB1与底面ABC所成二面角为锐角,
∴侧面A1ABB1与底面ABC所成二面角的大小为600.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
【题目】若在定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数有“和一点”
成立,则称函数有“和一点”![]() .
.
(1)函数![]() 是否有“和一点”?请说明理由;
是否有“和一点”?请说明理由;
(2)若函数![]() 有“和一点”,求实数
有“和一点”,求实数![]() 的取值范围;
的取值范围;
(3)求证:![]() 有“和一点”.
有“和一点”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三年级在一次理科综合检测中统计了部分“住校生”和“非住校生”共20人的物理、化学的成绩制成下列散点图(物理成绩用![]() 表示,化学成绩用
表示,化学成绩用![]() 表示)(图1)和生物成绩的茎叶图(图2).
表示)(图1)和生物成绩的茎叶图(图2).
![]()
![]()

(图1)
住校生 非住校生
2 6
9 8 5 4 4 3 1 7 4 5 7 7 9 9
6 5 8 2 2 5 7
(图2)
(1)若物理成绩高于90分,我们视为“优秀”,那么以这20人为样本,从物理成绩优秀的人中随机抽取2人,求至少有1人是住校生的概率;
(2)若化学成绩高于80分,我们视为“优秀”,根据图1完成如下列联表,并判断是否有95%的把握认为优秀率与住校有关;
住校 | 非住校 | |
优 秀 | ||
非优秀 |
附:(![]() ,其中
,其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)若生物成绩高于75分,我们视为“良好”,将频率视为概率,若从全年级学生中任选3人,记3人中生物成绩为“良好”的学生人数为随机变量![]() ,求出
,求出![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)时间经过![]() (时),时针、分针各转了多少度?各等于多少弧度?
(时),时针、分针各转了多少度?各等于多少弧度?
(2)有人说,钟的时针和分针一天内会重合24次。你认为这种说法是否正确?请说明理由.
(提示:从午夜零时算起,假设分针走了t min会与时针重合,一天内分针和时针会重合n次,建立t关于n的函数解析式,并画出其图象,然后求出每次重合的时间)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点M.设
相交于点M.设![]() ,
,![]() .
.

(1)试用向量![]() 表示
表示![]() .
.
(2)在线段![]() 上取点E,在线段
上取点E,在线段![]() 取点F,使
取点F,使![]() 过点M.设
过点M.设![]() ,
,![]() ,其中
,其中![]() 当
当![]() 与
与![]() 重合时,
重合时,![]() ,
,![]() ,此时
,此时![]() ;当
;当![]() 与
与![]() 重合时,
重合时,![]() ,
,![]() ,此时
,此时![]() .能否由此得出般结论:不论
.能否由此得出般结论:不论![]() 在线段
在线段![]() 上如何变动,等式
上如何变动,等式![]() 恒成立,请说明理由.
恒成立,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系.已知曲线
轴的正半轴为极轴,建立极坐标系.已知曲线![]() :
:![]() (
(![]() 为参数),
为参数), ![]() :
:![]() (
(![]() 为参数).
为参数).
(1)化![]() ,
,![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() ,
,![]() 为
为![]() 上的动点,求线段
上的动点,求线段![]() 的中点
的中点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣3|+x+1.
(1)求函数f(x)的最小值;
(2)当x≥1时,关于x的不等式f(2x)<4x+2a恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学为了计算函数![]() 图象与x轴,直线
图象与x轴,直线![]() ,
,![]() 所围成形状A的面积,采用“随机模拟方法”,用计算机分别产生10个在
所围成形状A的面积,采用“随机模拟方法”,用计算机分别产生10个在![]() 上的均匀随机数
上的均匀随机数![]() 和10个在
和10个在![]() 上的均匀随机数
上的均匀随机数![]() ,其数据记录为如下表的前两行.
,其数据记录为如下表的前两行.
| 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
(1)依据表格中的数据回答,在图形A内的点有多少个,分别是什么?
(2)估算图形A的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地煤气公司规定,居民每个月使用的煤气费由基本月租费、保险费和超额费组成.每个月的保险费为3元,当每个月使用的煤气量不超过am3时,只缴纳基本月租费c元;如果超过这个使用量,超出的部分按b元/m3计费.
(1)请写出每个月的煤气费y(元)关于该月使用的煤气量x(m3)的函数解析式;
(2)如果某个居民7~9月份使用煤气与收费情况如下表,请求出a,b,c,并画出函数图象;
月份 | 煤气使用量/m3 | 煤气费/元 |
7 | 4 | 4 |
8 | 10 | 10 |
9 | 16 | 19 |
其中,仅7月份煤气使用量未超过am3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com