
【题目】如图,2012年春节,摄影爱好者![]() 在某公园
在某公园![]() 处,发现正前方
处,发现正前方![]() 处有一立柱,测得立柱顶端
处有一立柱,测得立柱顶端![]() 的仰角和立柱底部
的仰角和立柱底部![]() 的俯角均为
的俯角均为![]() ,设
,设![]() 的眼睛距地面的距离
的眼睛距地面的距离![]() 米.
米.
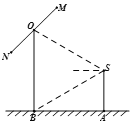
(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆![]() 绕其中点
绕其中点![]() 在
在![]() 与立柱所在的平面内旋转.摄影者有一视角范围为
与立柱所在的平面内旋转.摄影者有一视角范围为![]() 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
【答案】(1)![]() ,
,![]() ;(2)摄影者可以将彩杆全部摄入画面.
;(2)摄影者可以将彩杆全部摄入画面.
【解析】
试题分析:(1)摄影者眼部记为点![]() ,作
,作![]() 于
于![]() ,则有
,则有![]() ,
,![]() .
.![]() ,在
,在![]() 中,由三角函数的定义可求
中,由三角函数的定义可求![]() ;再由
;再由![]() ,
,![]() ,在
,在![]() 中由三角函数的定义可求
中由三角函数的定义可求![]() ,进而可求
,进而可求![]() ;(2)以
;(2)以![]() 为原点,以水平方向向右为
为原点,以水平方向向右为![]() 轴正方向建立平面直角坐标系.设
轴正方向建立平面直角坐标系.设![]() ,
,![]() ,则
,则![]() ,由(1)知
,由(1)知![]() ,利用向量的数量积的坐标表示可求
,利用向量的数量积的坐标表示可求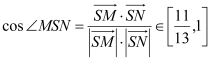 ,结合余弦函数的性质可求答案.
,结合余弦函数的性质可求答案.
试题解析:(1)作![]() 垂直
垂直![]() 于
于![]() ,则
,则![]() ,
,![]() .
.
又![]() ,故在
,故在![]() 中,可求得
中,可求得![]() ,即摄影者到立柱的水平距离为
,即摄影者到立柱的水平距离为![]() 米.
米.
由![]() ,
,![]() ,在
,在![]() 中,可求得
中,可求得![]() .
.
因为![]() ,故
,故![]() ,即立柱高为
,即立柱高为![]() 米.
米.
(2)如图,![]() 为原点,以水平方向向右为
为原点,以水平方向向右为![]() 轴正方向建立平面直角坐标系.
轴正方向建立平面直角坐标系.
设![]() ,
,![]() ,则
,则![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() .
.
故![]() ,
,![]() ,
,
∴![]()
![]()
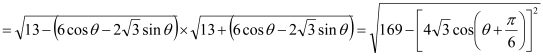

由![]() 知
知![]() 所以
所以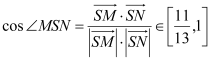 ,
,
∴![]() 恒成立
恒成立
故在彩杆转动的任意时刻,摄影者都可以将彩杆全部摄入画面


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明{an+ ![]() }是等比数列,并求{an}的通项公式;
}是等比数列,并求{an}的通项公式;
(2)证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过直线x﹣y﹣1=0与直线2x+y﹣5=0的交点P.
(1)若l与直线x+3y﹣1=0垂直,求l的方程;
(2)点A(﹣1,3)和点B(3,1)到直线l的距离相等,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点.已知a,b是实数,1和-1是函数f(x)=x3+ax2+bx的两个极值点.
(1)求a和b的值;
(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,若
中,若![]() 是线段
是线段![]() 上的动点,则下列结论不正确的是( )
上的动点,则下列结论不正确的是( )

A. 三棱锥![]() 的正视图面积是定值
的正视图面积是定值
B. 异面直线![]() 所成的角可为
所成的角可为![]()
C. 三棱锥![]() 的体积大小与点
的体积大小与点![]() 在线段
在线段![]() 的位置有关
的位置有关
D. 直线![]() 与平面
与平面![]() 所成的角可为
所成的角可为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com