
【题目】如图所示,在棱长为4的正方体ABCD﹣A1B1C1D1中,点E是棱CC1的中点,则异面直线D1E与AC所成角的余弦值是 . 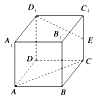
科目:高中数学 来源: 题型:
【题目】为了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位三十岁到四十岁的公务员,得到如下列联表,因不慎丢失部分数据.
(1)完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省妇联的人数为X,求X的分布列及数学期望E(X).
男性公务员 | 女性公务员 | 总计 | |
有意愿生二胎 | 15 | 45 | |
无意愿生二胎 | 25 | ||
总计 |
P(k2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
附: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品的市场需求量![]() (万件)、市场供应量
(万件)、市场供应量![]() (万件)与市场价格
(万件)与市场价格![]() (元/件)分别近似地满足下列关系:
(元/件)分别近似地满足下列关系: ![]() ,
, ![]() .当
.当![]() 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
(1)求平衡价格和平衡需求量;
(2)若该商品的市场销售量![]() (万件)是市场需求量
(万件)是市场需求量![]() 和市场供应量
和市场供应量![]() 两者中的较小者,该商品的市场销售额
两者中的较小者,该商品的市场销售额![]() (万元)等于市场销售量
(万元)等于市场销售量![]() 与市场价格
与市场价格![]() 的乘积.
的乘积.
①当市场价格![]() 取何值时,市场销售额
取何值时,市场销售额![]() 取得最大值;
取得最大值;
②当市场销售额![]() 取得最大值时,为了使得此时的市场价格恰好是新的市场平衡价格,则政府应该对每件商品征税多少元?
取得最大值时,为了使得此时的市场价格恰好是新的市场平衡价格,则政府应该对每件商品征税多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数
是奇函数
(Ⅰ)求![]() 值;
值;
(Ⅱ)判断并证明该函数在定义域![]() 上的单调性;
上的单调性;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅳ)设关于![]() 的函数
的函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是圆柱底面圆的直径,
是圆柱底面圆的直径, ![]() 是底面圆周上异于
是底面圆周上异于![]() 的任意一点,
的任意一点, ![]() .
.
(1)求证: ![]() ;
;
(2)求三棱锥![]() 体积的最大值,并写出此时三棱锥
体积的最大值,并写出此时三棱锥![]() 外接球的表面积.
外接球的表面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(Ⅰ)若此方程表示圆,求![]() 的取值范围;
的取值范围;
(Ⅱ)若(Ⅰ)中的圆与直线![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线过点P(﹣3 ![]() ,4),它的渐近线方程为y=±
,4),它的渐近线方程为y=± ![]() x.
x.
(1)求双曲线的标准方程;
(2)设F1和F2为该双曲线的左、右焦点,点P在此双曲线上,且|PF1||PF2|=41,求∠F1PF2的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆 ![]() 上任取一点
上任取一点 ![]() ,点
,点 ![]() 在
在 ![]() 轴的正射影为点
轴的正射影为点 ![]() ,当点
,当点 ![]() 在圆上运动时,动点
在圆上运动时,动点 ![]() 满足
满足 ![]() ,动点
,动点 ![]() 形成的轨迹为曲线
形成的轨迹为曲线 ![]() .
.
(Ⅰ)求曲线 ![]() 的方程;
的方程;
(Ⅱ)点 ![]() 在曲线
在曲线 ![]() 上,过点
上,过点 ![]() 的直线
的直线 ![]() 交曲线
交曲线 ![]() 于
于 ![]() 两点,设直线
两点,设直线 ![]() 斜率为
斜率为 ![]() ,直线
,直线 ![]() 斜率为
斜率为 ![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com