【题目】设抛物线C：
的焦点为F，经过点F的直线与抛物线交于A、B两点．
(1)若
，求线段
中点M的轨迹方程；
(2)若直线AB的方向向量为
，当焦点为
时，求
的面积；
(3)若M是抛物线C准线上的点，求证：直线
的斜率成等差数列．
全优点练单元计划系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，已知椭圆C：
(a>b>0)的离心率为
，右焦点F到右准线的距离为3.
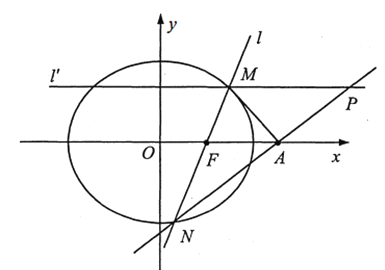
（1）求椭圆C的方程;
（2）过点F作直线l (不与x 轴重合)和椭圆C交于M， N两点，设点
.
①若
的面积为
，求直线l方程；
②过点M作与)轴垂直的直线l"和直线NA交于点P，求证：点P在一条定直线上.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】曲线
为：到两定点
、
距离乘积为常数
的动点
的轨迹.以下结论正确的个数为（ ）
（1）曲线一定经过原点；
（2）曲线关于
轴、
轴对称；
（3）
的面积不大于
；
（4）曲线在一个面积为
的矩形范围内.
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某烘焙店加工一个成本为60元的蛋糕，然后以每个120元的价格出售，如果当天卖不完，剩下的这种蛋糕作餐厨垃圾处理.
（1）若烘焙店一天加工16个这种蛋糕，，求当天的利润
（单位：元）关于当天需求量
（单位：个，
）的函数解析式；
（2）烘焙店记录了100天这种蛋糕的日需求量（单位：个），整理得下表：
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若烘焙店一天加工16个这种蛋糕，
表示当天的利润（单位：元），求的分布列与数学期望及方差；
②若烘焙店一天加工16个或17个这种蛋糕，仅从获得利润大的角度考虑，你认为应加工16个还是17个？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校积极开展“服务社会，提升自我”的志愿者服务活动，九年级的五名同学(三男两女)成立了“交通秩序维护”小分队．若从该小分队中任选两名同学进行交通秩序维护，则恰是一男一女的概率是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两人同时参加一个外贸公司的招聘,招聘分笔试与面试两部分,先笔试后面试.甲笔试与面试通过的概率分别为0.8,0.5,乙笔试与面试通过的概率分别为0.8,0.4,且笔试通过了才能进入面试,面试通过则直接招聘录用,两人笔试与面试相互独立互不影响.
(1)求这两人至少有一人通过笔试的概率;
(2)求这两人笔试都通过却都未被录用的概率;
(3)记这两人中最终被录用的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
）.
（1）证明：当
时，
在
上是增函数；
（2）是否存在实数
，只有唯一正数
，对任意正数
，使不等式
恒成立？若存在，求出这样的；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
