
| A. | $\frac{1}{128}$ | B. | $\frac{1}{256}$ | C. | $\frac{1}{512}$ | D. | $\frac{3}{4}$ |
分析 由已知函数f(x)满足的三个条件求出f(1),f($\frac{1}{2}$),f($\frac{1}{3}$),进而求出f($\frac{1}{9}$),f($\frac{1}{6}$)的函数值,又由函数f(x)为非减函数,求出f($\frac{1}{8}$)的值,即可得到f($\frac{1}{3}$)+f($\frac{1}{8}$)的值.
解答 解:∵函数f(x)在[0,1]上为非减函数,①f(0)=0;③f(1-x)+f(x)=1,∴f(1)=1,
令x=$\frac{1}{2}$,所以有f($\frac{1}{2}$)=$\frac{1}{2}$.
又∵②f($\frac{x}{3}$)=$\frac{1}{2}$f(x),∴f(x)=2f($\frac{x}{3}$),∴令=1,可得1=2f($\frac{1}{3}$),∴f($\frac{1}{3}$)=$\frac{1}{2}$.
令x=$\frac{1}{2}$,可得f($\frac{1}{6}$)=$\frac{1}{2}$f($\frac{1}{2}$)=$\frac{1}{4}$,令x=$\frac{1}{3}$,可得f($\frac{1}{9}$)=$\frac{1}{2}$f($\frac{1}{3}$)=$\frac{1}{4}$.
∵当x1<x2时都有f(x1)≤f(x2),$\frac{1}{9}$<$\frac{1}{8}$<$\frac{1}{6}$,∴f($\frac{1}{9}$)≤f($\frac{1}{8}$)≤f($\frac{1}{6}$ ),∴f($\frac{1}{8}$)=$\frac{1}{4}$,
∴f($\frac{1}{3}$)+f($\frac{1}{8}$)=$\frac{1}{2}$+$\frac{1}{4}$=$\frac{3}{4}$,
故选:D.
点评 本题主要考查抽象函数、新定义的应用,充分利用题意中非减函数性质,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
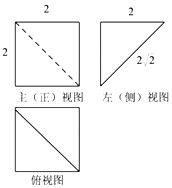
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{{8\sqrt{2}}}{3}$ | D. | $\frac{{4\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩 | 人数 |
| A | 9 |
| B | 12 |
| C | 31 |
| D | 22 |
| E | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | ±3 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com