
【题目】如果一个点是一个指数函数和一个对数函数的图像的交点,那么称这个点为"好点".下列四个点P1(1,1),P2(1,2),P3(![]() ,
,![]() ),P4(2,2)中,"好点"有( )个
),P4(2,2)中,"好点"有( )个
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
可设指数函数为y=ax,对数函数为y=logbx,容易判断P1,P2不在对数函数图象上,从而判断这两点不是“好点”,然后将P3的坐标分别代入指数函数和对数函数解析式,从而可解出a,b,进而判断出P3为“好点”,同样的方法可判断P4为好点,进而找出正确选项.
设指数函数为y=ax,对数函数为y=logbx;
对于对数函数,x=1时,y=0,则P1,P2不是对数函数图象上的点;
∴P1,P2不是好点;
将P3的坐标分别代入指数函数和对数函数解析式得:
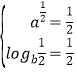 ;
;
解得![]() ;
;
即P3是指数函数![]() 和对数函数
和对数函数![]() 的交点,即P3为“好点”;
的交点,即P3为“好点”;
同样,将P4坐标代入函数解析式得:
![]() ;
;
解得![]() ;
;
∴P4是“好点”;
∴“好点”个数为2.
故选:B.


科目:高中数学 来源: 题型:
【题目】学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
A. 6种 B. 24种 C. 30种 D. 36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() 的斜率互为相反数.
的斜率互为相反数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场去年国庆期间累计生成![]() 万张购物单,从中随机抽出
万张购物单,从中随机抽出![]() 张,对每单消费金额进行统计得到下表:
张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 |
由于工作人员失误,后两栏数据无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题:
(1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过![]() 元的概率;
元的概率;
(2)为鼓励顾客消费,该商场计划在今年国庆期间进行促销活动,凡单笔消费超过![]() 元者,可抽奖一次.抽奖规则为:从装有大小材质完全相同的
元者,可抽奖一次.抽奖规则为:从装有大小材质完全相同的![]() 个红球和
个红球和![]() 个黑球的不透明口袋中,随机摸出
个黑球的不透明口袋中,随机摸出![]() 个小球,并记录两种颜色小球的数量差的绝对值
个小球,并记录两种颜色小球的数量差的绝对值![]() ,当
,当![]() 时,消费者可分别获得价值
时,消费者可分别获得价值![]() 元、
元、![]() 元和
元和![]() 元的购物券.求参与抽奖的消费者获得购物券的价值的数学期望.
元的购物券.求参与抽奖的消费者获得购物券的价值的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128 dm2,上、下两边各空2 dm,左、右两边各空1 dm.如何设计海报的尺寸,才能使四周空白面积最小?
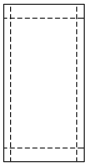
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 中点.将
中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图2).
(如图2).

(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出
? 若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com