
【题目】设函数![]() 的导函数为
的导函数为![]() .若不等式
.若不等式![]() 对任意实数x恒成立,则称函数
对任意实数x恒成立,则称函数![]() 是“超导函数”.
是“超导函数”.
(1)请举一个“超导函数” 的例子,并加以证明;
(2)若函数![]() 与
与![]() 都是“超导函数”,且其中一个在R上单调递增,另一个在R上单调递减,求证:函数
都是“超导函数”,且其中一个在R上单调递增,另一个在R上单调递减,求证:函数![]() 是“超导函数”;
是“超导函数”;
(3)若函数![]() 是“超导函数”且方程
是“超导函数”且方程![]() 无实根,
无实根,![]() (e为自然对数的底数),判断方程
(e为自然对数的底数),判断方程![]() 的实数根的个数并说明理由.
的实数根的个数并说明理由.
【答案】(1)见解析.
(2)见解析.
(3)见解析.
【解析】分析:(1)根据定义举任何常数都可以;(2)∵![]() ,∴
,∴![]() ,即证
,即证![]() -
-![]() 在R上成立即可;(3)构造函数
在R上成立即可;(3)构造函数![]() ,因为
,因为![]() 是“超导函数”, ∴
是“超导函数”, ∴![]() 对任意实数
对任意实数![]() 恒成立,而方程
恒成立,而方程![]() 无实根,故
无实根,故![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递减, 故方程
上单调递减, 故方程![]() 等价于
等价于![]() ,即
,即![]() ,
,
设![]()
![]() ,分析函数单调性结合零点定理即可得出结论.
,分析函数单调性结合零点定理即可得出结论.
详解:
(1)举例:函数![]() 是“超导函数”,
是“超导函数”,
因为![]() ,
,![]() ,满足
,满足![]() 对任意实数
对任意实数![]() 恒成立,故
恒成立,故![]() 是“超导函数”.
是“超导函数”.
注:答案不唯一,必须有证明过程才能给分,无证明过程的不给分.
(2)∵![]() ,∴
,∴![]() ,
,
∴![]()
![]()
因为函数![]() 与
与![]() 都是“超导函数”,所以不等式
都是“超导函数”,所以不等式![]() 与
与![]() 对任意实数
对任意实数![]() 都恒成立,故
都恒成立,故![]() ,
,![]() ,①
,①
而![]() 与
与![]() 一个在
一个在![]() 上单调递增,另一个在
上单调递增,另一个在![]() 上单调递减,故
上单调递减,故![]() ,②
,②
由①②得![]() 对任意实数
对任意实数![]() 都恒成立,所以函数
都恒成立,所以函数![]() 是“超导函数”.
是“超导函数”.
(3)∵![]() ,所以方程
,所以方程![]() 可化为
可化为![]() ,
,
设函数![]() ,
,![]() ,则原方程即为
,则原方程即为![]() ,③
,③
因为![]() 是“超导函数”, ∴
是“超导函数”, ∴![]() 对任意实数
对任意实数![]() 成立,
成立,
而方程![]() 无实根,故
无实根,故![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递减,
上单调递减,
故方程③等价于![]() ,即
,即![]() ,
,
设![]()
![]() ,
,![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
故![]() 在
在![]() 上单调递增,
上单调递增,
而![]() ,
,![]() ,且函数
,且函数![]() 的图象在
的图象在![]() 上连续不断,
上连续不断,
故![]()
![]() 在
在![]() 上有且仅有一个零点,从而原方程有且仅有唯一实数根.
上有且仅有一个零点,从而原方程有且仅有唯一实数根.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知正项数列{an} 为等比数列,等差数列{bn} 的前n 项和为Sn (n∈N* ),且满足:S13=208,S9﹣S7=41,a1=b2,a3=b3.
(1)求数列{an},{bn} 的通项公式;
(2)设Tn=a1b1+a2b2+…+anbn (n∈N* ),求Tn;
(3)设![]() ,是否存在正整数m,使得cm·cm+1·cm+2+8=3(cm+cm+1+cm+2).
,是否存在正整数m,使得cm·cm+1·cm+2+8=3(cm+cm+1+cm+2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() ,
,![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() ,
,![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年时红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神.首先在甲、乙、丙、丁四个不同的公园进行支持签名活动,其次在各公园签名的人中按分层抽样的方式抽取10名幸运之星,每人获得一个纪念品,其数据表格如下:

(Ⅰ)求此活动中各公园幸运之星的人数;
(Ⅱ)从乙和丙公园的幸运之星中任选两人接受电视台记者的采访,求这两人均来自乙公园的概率;
(Ⅲ)电视台记者对乙公园的签名人进行了是否有兴趣研究“红军长征”历史的问卷调查,统计结果如下(单位:人):

据此判断能否在犯错误的概率不超过0.01的前提下认为有兴趣研究“红军长征”历史与性别有关.
附临界值表及公式:  ,其中
,其中![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系xoy中,椭圆![]() 的离心率为
的离心率为![]() ,过点
,过点![]() .
.
(1)求椭圆C的方程;
(2)已知点P(2,1),直线![]() 与椭圆C相交于A,B两点,且线段AB被直线OP平分.
与椭圆C相交于A,B两点,且线段AB被直线OP平分.
①求直线![]() 的斜率;②若
的斜率;②若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了巩固全国文明城市创建成果,今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度,随机从存在违章搭建的户主中抽取了男性、女性共![]() 名进行调查,调查结果如下:
名进行调查,调查结果如下:
支持 | 反对 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
(1)根据以上数据,判断是否有![]() 的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
(2)现从参与调查的女户主中按分层抽样的方法抽取![]() 人进行调查,分别求出所抽取的
人进行调查,分别求出所抽取的![]() 人中持“支持”和“反对”态度的人数;
人中持“支持”和“反对”态度的人数;
(3)现从(2)中所抽取的![]() 人中,再随机抽取
人中,再随机抽取![]() 人赠送小品,求恰好抽到
人赠送小品,求恰好抽到![]() 人持“支持”态度的概率?
人持“支持”态度的概率?
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
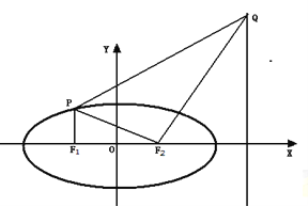
【题目】如图,点![]() 分别是椭圆C:
分别是椭圆C:![]() 的左、右焦点,过点
的左、右焦点,过点![]() 作
作![]() 轴的垂线,交椭圆
轴的垂线,交椭圆![]() 的上半部分于点
的上半部分于点![]() ,过点
,过点![]() 作
作![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() .
.
(1)如果点![]() 的坐标为(4,4),求椭圆
的坐标为(4,4),求椭圆![]() 的方程;
的方程;
(2)试判断直线![]() 与椭圆
与椭圆![]() 的公共点个数,并证明你的结论.
的公共点个数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com