
����Ŀ��ij�ؼƻ���һ����̲����һ����ֳ��.
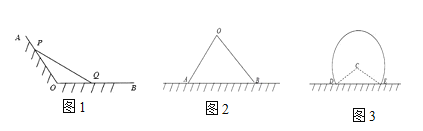
��1����ͼ1������OA��OBΪ�����ߣ�![]() �����ó���Ϊ1ǧ��Χ��PQ���к�����Χ��һ��
�����ó���Ϊ1ǧ��Χ��PQ���к�����Χ��һ��![]() ����ֳ���������ѡȡ��P��Q������ʹ��ֳ��
����ֳ���������ѡȡ��P��Q������ʹ��ֳ��![]() ������������������.
������������������.
��2����ͼ2��ֱ��lΪ�����ߣ����ó���Ϊ1ǧ��Χ�����к�����Χ��һ����ֳ��.����һ��Χ��������OAB����A��B��ֱ��l�ϣ���ʹ������OAB����������Ϊ![]() ����������Χ�ɹ���CDE����D��E��ֱ��l�ϣ�C���Ż�����Բ��Բ����
����������Χ�ɹ���CDE����D��E��ֱ��l�ϣ�C���Ż�����Բ��Բ����![]() ���������Ϊ
���������Ϊ![]() �������
�������![]() �����ֵ��
�����ֵ��![]() ������ȷ��0.01ƽ��ǧ�ף�����ָ����һ����Ʒ�������.
������ȷ��0.01ƽ��ǧ�ף�����ָ����һ����Ʒ�������.
���𰸡���1��![]() ��
��![]() ƽ��ǧ�ף�2��
ƽ��ǧ�ף�2��![]() ƽ��ǧ�ף�
ƽ��ǧ�ף�![]() ԼΪ0.144ƽ��ǧ�ף�����������.
ԼΪ0.144ƽ��ǧ�ף�����������.
��������
��1����![]()
![]() ����
����![]() �������û�������ʽ��������������������㹫ʽ���ɵó�.
�������û�������ʽ��������������������㹫ʽ���ɵó�.
��2������һ����![]()
![]() ����
����![]() .��
.��![]() �����û�������ʽ�����ʼ��ɵó����ֵ.
�����û�������ʽ�����ʼ��ɵó����ֵ.
����������뾶![]()
![]() ����
����![]() .���
.���![]() .
.
�ɵ�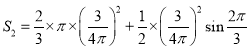 �����ɱȽϳ�
�����ɱȽϳ�![]() ��
��![]() �Ĵ�С��ϵ.
�Ĵ�С��ϵ.
�⣺��1����![]()
![]() ��
��
��![]() ��
��
�ɵ�![]() ��
��
���ҽ���![]() ʱȡ�Ⱥ�.
ʱȡ�Ⱥ�.
![]()
![]() .
.
![]() ���ҽ���
���ҽ���![]() ʱ��
ʱ��
��ֳ��![]() ��������
��������![]() ��ƽ��ǧ�ף�
��ƽ��ǧ�ף�
��2������һ����![]()
![]() ��
��
��![]() .
.
��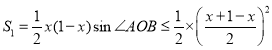
![]() ��
��
���ҽ���![]() ʱȡ�Ⱥ�.
ʱȡ�Ⱥ�.
![]() ��ƽ��ǧ�ף���
��ƽ��ǧ�ף���
����������뾶![]()
![]() ��
��
��![]() .���
.���![]() .
.
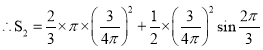
![]() ��ƽ��ǧ�ף�
��ƽ��ǧ�ף�
![]() ����������Χ�ɵ���ֳ������ϴ���������.
����������Χ�ɵ���ֳ������ϴ���������.


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ӳ�����������Ϸ���������ϱ��е�1վ����2վ����3վ��������100վ����100վ��������������![]() վ�ĸ���Ϊ
վ�ĸ���Ϊ![]() ��һö���ӿ�ʼ�ڵ�1վ������ÿ��һ��Ӳ�ң�������ǰ����һ��.��Ӳ�ҵ��������ϣ�������ǰ��һվ����Ӳ�ҵķ������ϣ�������ǰ����վ��ֱ������������99վ��ʧ�ܣ����ߵ�100վ����ʤ��ʱ����Ϸ����.
��һö���ӿ�ʼ�ڵ�1վ������ÿ��һ��Ӳ�ң�������ǰ����һ��.��Ӳ�ҵ��������ϣ�������ǰ��һվ����Ӳ�ҵķ������ϣ�������ǰ����վ��ֱ������������99վ��ʧ�ܣ����ߵ�100վ����ʤ��ʱ����Ϸ����.
��1����![]()
![]()
![]() ��
��
��2����֤������![]()
![]() Ϊ�ȱ����У�
Ϊ�ȱ����У�
��3���������Ϸ��ʤ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ����
����![]() ��
��![]() �ϴ�����㣬��ʵ��
�ϴ�����㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����������![]() ������
������![]() ʹ
ʹ![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������ʵ��![]() ��ʹ�õ�
��ʹ�õ�![]() ʱ��
ʱ��![]() ���������ʵ��
���������ʵ��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
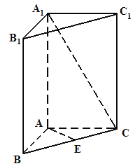
����Ŀ����ͼ��ֱ������![]() �ĵ���
�ĵ���![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ������
������![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() �����
�����
��1����ֱ������![]() ��ȫ�����
��ȫ�����
��2��������ֱ��![]() ��
��![]() ���ɽ�
���ɽ�![]() �Ĵ�С������÷����Ǻ�����ʾ����
�Ĵ�С������÷����Ǻ�����ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���![]() ��������������
��������������![]() ��ʹ�ö������
��ʹ�ö������![]() ������
������![]() ���������dzƺ���
���������dzƺ���![]() Ϊ��
Ϊ��![]() ͬ�Ȳ�����������
ͬ�Ȳ�����������
��1����֤��������������![]() ��
��![]() ��������
��������![]() ͬ�Ȳ�����������
ͬ�Ȳ�����������
��2��������![]() ����
����![]() ͬ�Ȳ�������������
ͬ�Ȳ�������������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���Ƿ����������![]() ��ʹ�ú���
��ʹ�ú���![]() Ϊ��
Ϊ��![]() ͬ�Ȳ����������������ڣ���
ͬ�Ȳ����������������ڣ���![]() ��ȡֵ��Χ���������ڣ���˵�����ɣ�
��ȡֵ��Χ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��![]() ��
��![]() ��Ϊʵ����
��Ϊʵ����![]() ���Ӽ����ǣ�
���Ӽ����ǣ�![]() ��
��
��1����֪![]() ��
��![]() �������оٷ���ʾ
�������оٷ���ʾ![]() ��
��
��2����![]() ����
����![]() ����
����![]() ʱ������
ʱ������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() �����
�����![]() ��
��![]() ����
����![]() �е�����Ԫ��֮��Ϊ
�е�����Ԫ��֮��Ϊ![]() ����������
����������![]() ����
����![]() ������������
������������![]() ��
��![]() ��
��![]() ������ʽ
������ʽ![]() ���������ʵ��
���������ʵ��![]() �����ֵ��
�����ֵ��
��3������������![]() �����
�����![]() Ϊ������������������һ����������Ϊ��������
Ϊ������������������һ����������Ϊ��������![]() ��ij���ǿ������Ӽ�������Ԫ�صĺͣ����
��ij���ǿ������Ӽ�������Ԫ�صĺͣ����![]() Ϊ��
Ϊ��![]() �Ļ��������ʣ��Ƿ����һ���������ϼ�������������
�Ļ��������ʣ��Ƿ����һ���������ϼ�������������![]() �Ļ�������˵�����ɣ�
�Ļ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����2acosB��2c��b��
��1�����A�Ĵ�С��
��2������ABC�����Բ�İ뾶Ϊ![]() �����Ϊ
�����Ϊ![]() �����ABC���ܳ���
�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x2��2xsin��+1�Ķ�������Բx2+my2=1�ϣ�����������������ֻ����������m��ȡֵ��Χ��_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɰ�Բ![]() �Ͳ���������
�Ͳ���������![]() �ϳɵ�����
�ϳɵ�����![]() ��Ϊ����ë���ߡ�������
��Ϊ����ë���ߡ�������![]() ��
��![]() ����
����![]() �������㣬�Ҿ�����
�������㣬�Ҿ�����![]()

(1)��![]() ��ֵ��
��ֵ��
(2)��![]()
![]() ����
Ϊ����![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����Сֵ��
����Сֵ��
(3)��![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ������ë���������ཻ�ڵ�
������ë���������ཻ�ڵ�![]() ���㣬���Ƿ����ʵ��
���㣬���Ƿ����ʵ��![]() ʹ��
ʹ��![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵�����ɡ�
��ֵ���������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com