
分析 过M作AM′⊥β垂足为M′,则MM′=$\sqrt{3}$,作MH⊥l,垂足为H,连接HM′,则l⊥M′H,∠MHM′为锐二面角α-l-β的平面角,在直角△MHM′中求解即可.
解答 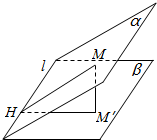 解:过M作AM′⊥β垂足为M′,则MM′=$\sqrt{3}$,作MH⊥l,垂足为H,连接HM′,
解:过M作AM′⊥β垂足为M′,则MM′=$\sqrt{3}$,作MH⊥l,垂足为H,连接HM′,
则l⊥M′H,∠MHM′为锐二面角α-l-β的平面角,
在直角△MHM′中,sin∠MHM′=$\frac{\sqrt{3}}{MH}$=$\frac{\sqrt{3}}{2}$,
∴M′H=2.
点评 本题考查二面角的大小度量,考查转化、空间想象、计算能力.本题找出,∠MHM′为锐二面角α-l-β的平面是关键.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2=2 | B. | 9<x3•x4<25 | C. | 0<(6-x3)•(6-x4)<1 | D. | 1<x1•x2<9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=($\sqrt{x}$)2 | B. | y=($\root{3}{x}$)3 | C. | y=$\sqrt{{x}^{2}}$ | D. | y=$\root{3}{{x}^{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com