
| 价格 | 14 | 16 | 18 | 20 | 22 |
| 需求量 | 12 | 10 | 12 | 5 | 3 |
分析 根据题目中的数据,求出$\overline{x}$、$\overline{y}$与$\underset{\stackrel{5}{∑}}{i=1}$xiyi、$\sum_{i=1}^{5}$${{x}_{i}}^{2}$,代入公式计算回归方程系数$\stackrel{∧}{b}$与$\stackrel{∧}{a}$,即可求出线性回归方程.
解答 解:∵$\overline{x}$=$\frac{1}{5}$×(14+16+18+20+22)=18,
$\overline{y}$=$\frac{1}{5}$×(12+10+12+5+3)=8.4,
$\underset{\stackrel{5}{∑}}{i=1}$xiyi=14×12+16×10+18×12+20×5+22×3=710,
$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=142+162+182+202+222=1660;
∴$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{5}x}_{i}y}_{i}-5\overline{x}•\overline{y}}{{{\sum_{i=1}^{5}x}_{i}}^{2}-{5(\overline{x})}^{2}}$=$\frac{710-5×18×8.4}{1660-5{×18}^{2}}$=-1.15,
∴$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=8.4-(-1.15×18)=29.1;
∴所求的线性回归方程是$\stackrel{∧}{y}$=-1.15x+29.1.
点评 本题考查了线性回归方程的求法问题,解题时应根据公式进行计算,是基础题目.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | .035 | B. | 0.5 | C. | 0.75 | D. | 0.95 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
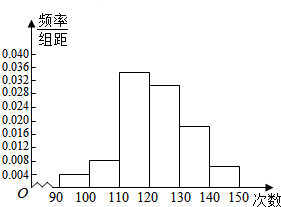 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.则 样本容量为150.
为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.则 样本容量为150.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
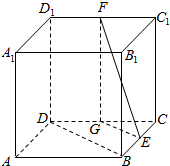 已知E,F分别是棱长为a的正方体ABCD-A1B1C1D1中的棱BC和C1D1的中点,求:
已知E,F分别是棱长为a的正方体ABCD-A1B1C1D1中的棱BC和C1D1的中点,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com