
【题目】如图,四边形![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() .四边形
.四边形![]() 是平行四边形,且
是平行四边形,且![]() .点
.点![]() ,
,![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,![]() ,且
,且![]() 在
在![]() 上,四棱锥
上,四棱锥![]() 的体积为2.
的体积为2.
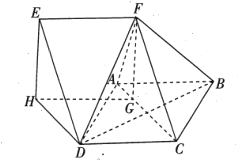
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?如果存在,是确定点
?如果存在,是确定点![]() 的位置,如果不存在,请说明理由.
的位置,如果不存在,请说明理由.
【答案】(1)见解析;(2)![]() 是靠近点
是靠近点![]() 的四等分点,理由见解析
的四等分点,理由见解析
【解析】
(1)先由线面垂直的判定定理,证明![]() 平面
平面![]() ,再由面面垂直的判定定理,即可证明结论成立;
,再由面面垂直的判定定理,即可证明结论成立;
(2)先由四棱锥的体积求出![]() ,得出
,得出![]() ,即点
,即点![]() 是靠近点
是靠近点![]() 的四等分点,延长
的四等分点,延长![]() 交
交![]() 于点
于点![]() ,在梯形
,在梯形![]() 内,过
内,过![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,则点
,则点![]() 即为所求,再由
即为所求,再由![]() ,即可确定点
,即可确定点![]() 的位置.
的位置.
(1)![]() 点
点![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
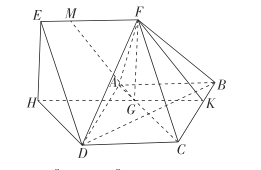
(2)假设在![]() 上是存在点
上是存在点![]() ,使
,使![]() 平面
平面![]() ,
,
![]() 四棱锥
四棱锥![]() 的体积为2,即
的体积为2,即![]() ,
,
![]() ,又
,又![]() ,
,![]() ,即点
,即点![]() 是靠近点
是靠近点![]() 的四等分点.
的四等分点.
延长![]() 交
交![]() 于点
于点![]() ,在梯形
,在梯形![]() 内,过
内,过![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,
,
则点![]() 即为所求.
即为所求.
![]() ,即点
,即点![]() 是靠近点
是靠近点![]() 的四等分点.
的四等分点.


科目:高中数学 来源: 题型:
【题目】设![]() 是定义在R上的两个周期函数,
是定义在R上的两个周期函数,![]() 的周期为4,
的周期为4,![]() 的周期为2,且
的周期为2,且![]() 是奇函数.当
是奇函数.当![]() 时,
时,![]() ,
, ,其中k>0.若在区间(0,9]上,关于x的方程
,其中k>0.若在区间(0,9]上,关于x的方程![]() 有8个不同的实数根,则k的取值范围是_____.
有8个不同的实数根,则k的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,有下述命题:①若
,有下述命题:①若![]() 是奇函数,则
是奇函数,则![]() 的图象关于点
的图象关于点![]() 对称;②函数
对称;②函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 为偶函数;③若对
为偶函数;③若对![]() ,有
,有![]() ,则2是
,则2是![]() 的一个周期;④函数
的一个周期;④函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称.其中正确的命题是______.(写出所有正确命题的序号)
对称.其中正确的命题是______.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁和戊5名学生进行某种劳动技术比赛,决出了第1到第5名的名次.甲乙两名参赛者去询问成绩,回答者对甲说,“很遗憾,你和乙都没没有拿到冠军.”对乙说,“你当然不会是最差的.”从这个回答分析,甲是第五名的概率是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com