
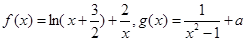
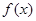 的单调区间.
的单调区间.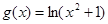 有4个不同的实根,求
有4个不同的实根,求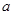 的范围?
的范围? ,使得关于
,使得关于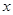 的方程
的方程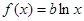 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b 满足的条件,如果不存在,说明理由.
满足的条件,如果不存在,说明理由. ,减区间为
,减区间为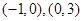 ;(2)
;(2)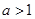 ;(3)不存在,理由见详解.
;(3)不存在,理由见详解. ,然后通过判断
,然后通过判断 的符号可求得单调区间;(2)构造函数
的符号可求得单调区间;(2)构造函数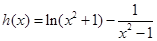 ,然后利用导数研究函数的取值变化,确定图象的位置,由图象可直观得到函
,然后利用导数研究函数的取值变化,确定图象的位置,由图象可直观得到函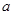 的取值范围;(3)
的取值范围;(3)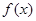 定义域后,求导得到
定义域后,求导得到 ,
,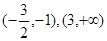 是函数
是函数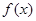 的增区间;在
的增区间;在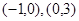 是函数
是函数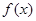 减区间.
减区间.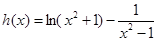 ,求导得
,求导得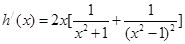 ,
, 和两个断点
和两个断点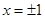 ,所以初步可以得到函数在区间
,所以初步可以得到函数在区间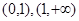 单调增;在区间
单调增;在区间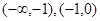 单调减.
单调减.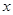 从负半轴方向趋近于-1时,
从负半轴方向趋近于-1时,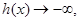
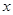 从正半轴方向趋近于-1时,
从正半轴方向趋近于-1时,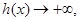
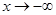 时,
时,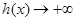 ,
,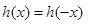 ,函数为偶函数,而且
,函数为偶函数,而且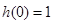 ,
,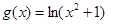 有4个不同的实根,结合图像得到
有4个不同的实根,结合图像得到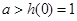 .
.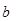 不存在.
不存在. ,使得方程
,使得方程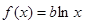 存在两个不相等的实根
存在两个不相等的实根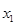 和
和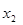 ,然后代入方程,根据其结构利用第(1)问的结论判断出
,然后代入方程,根据其结构利用第(1)问的结论判断出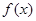 在
在 上的取值及单调性,然后结合假设导出矛盾,作出判断.
上的取值及单调性,然后结合假设导出矛盾,作出判断. ,使得方程
,使得方程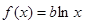 存在两个不相等的实根
存在两个不相等的实根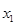 和
和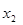 ,则
,则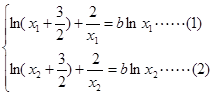
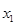 和
和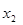 都是正数.
都是正数.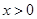 时,函数的最小值
时,函数的最小值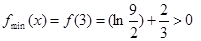 ,
,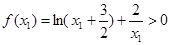 ,
,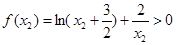
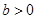 ,等式两边同号,所以,
,等式两边同号,所以,
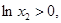 所以
所以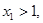
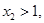
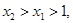
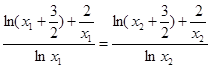 ,
,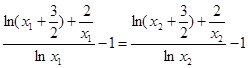 ,
,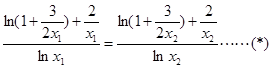 .
.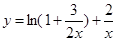 在
在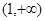 为恒大于0且为减函数
为恒大于0且为减函数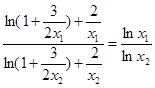 左边大于1,右边小于1.
左边大于1,右边小于1.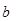 ,使得方程
,使得方程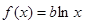 存在两个不相等的实根
存在两个不相等的实根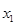 和
和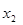 错误(本题其他证法,请酌情给分)
错误(本题其他证法,请酌情给分)

科目:高中数学 来源:不详 题型:填空题
 ③..y=f(x)的最小值为0,无最大值④.y=f(x)无最小值,最大值为sin1.正确的序号为.
③..y=f(x)的最小值为0,无最大值④.y=f(x)无最小值,最大值为sin1.正确的序号为.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,
,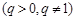 ;②
;② ;③
;③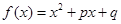 .
.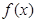 与月份x关系的函数模型为_________(填写相应函数的序号),若所选函数满足
与月份x关系的函数模型为_________(填写相应函数的序号),若所选函数满足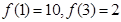 ,则
,则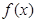 =_____________.
=_____________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 >0,给出下列命题:
>0,给出下列命题:查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 )<f(x)的x的取值范围是( )
)<f(x)的x的取值范围是( )| A.(2,+∞) | B.(-∞,-1) |
| C.[-2,-1)∪(2,+∞) | D.(-1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com