练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某市图书馆准备进一定量的书籍，由于不同年龄段对图书的种类需求不同，为了合理配备资源，现对该市看书人员随机抽取了一天60名读书者进行调查.将他们的年龄分成6段：，后得到如图所示的频率分布直方图，问：

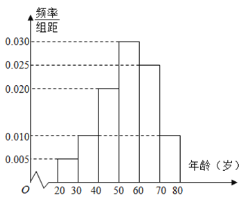
    （1）在60名读书者中年龄分布在的人数；

    （2）估计60名读书者年龄的平均数和中位数.

    【答案】（1）36人；（2）54，55.

    【解析】

    （1）从频率分布直方图中求出读书者中年龄分布在的频率，由此求得在60名读书者中年龄分布在的人数.

    （2）利用每组中点乘以对应的频率再相加，求得平均数的估计值；通过从左边开始，频率之和为的位置，由此求得中位数.

    （1）由频率分布直方图知年龄在的频率为，

    所以60名读书者中年龄分布在的人数为人.

    （2）60名读书者年龄的平均数为：

    ，

    设中位数为，则，

    解得，

    即60名读书者年龄的中位数为55.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆离心率为，点与椭圆的左、右顶点可以构成等腰直角三角形．点C是椭圆的下顶点，经过椭圆中心O的一条直线与椭圆交于A，B两个点（不与点C重合），直线CA，CB分别与x轴交于点D，E．

    （1）求椭圆的标准方程．

    （2）判断的大小是否为定值，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）讨论的单调性；

    （2）当时，若关于的不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂生产产品x件的总成本c（x）=1200+ x3（万元），已知产品单价P（万元）与产品件数x满足：p2= ，生产100件这样的产品单价为50万元．

    （1）设产量为x件时，总利润为L（x）（万元），求L（x）的解析式；

    （2）产量x定为多少件时总利润L（x）（万元）最大？并求最大值（精确到1万元）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：的离心率为，左、右顶点分别为A，B，点M是椭圆C上异于A，B的一点，直线AM与y轴交于点P．

    （Ⅰ）若点P在椭圆C的内部，求直线AM的斜率的取值范围；

    （Ⅱ）设椭圆C的右焦点为F，点Q在y轴上，且∠PFQ=90°，求证：AQ∥BM．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解中学生对交通安全知识的掌握情况，从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按，，，分组，得到的频率分布直方图.

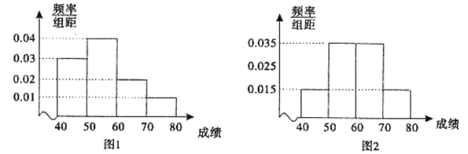
    （Ⅰ）分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩；

    （Ⅱ）完成下面列联表，并回答是否有的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”？

    成绩小于60分人数

    成绩不小于60分人数

    合计

    农村中学

    城镇中学

    合计

    附：

    临界值表：

    0.10

    0.05

    0.010

    2.706

    3.841

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．

    （1）若，求在处的切线方程；

    （2）若对于任意的正数，恒成立，求实数的值；

    （3）若函数存在两个极值点，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在四边形ABCD中，AD∥BC，BC=2AD，E，F分别为AD，BC的中点，AE=EF，．将四边形ABFE沿EF折起，使平面ABFE⊥平面EFCD（如图2），G是BF的中点．

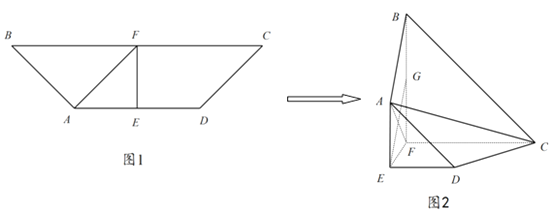
    （1）证明：AC⊥EG；

    （2）在线段BC上是否存在一点H，使得DH∥平面ABFE？若存在，求的值；若不存在，说明理由；

    （3）求二面角D-AC-F的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    （1）求函数的单调区间；

    （2）若函数存在两个极值点，，且，证明：．

    查看答案和解析>>

    同步练习册答案