
【题目】如图所示,倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线交于
,且与抛物线交于![]() 两点.
两点.
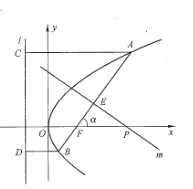
(1)求抛物线的焦点![]() 的坐标及准线
的坐标及准线![]() 的方程;
的方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 轴于点
轴于点![]() .证明
.证明![]() 为定值,并求此定值.
为定值,并求此定值.
科目:高中数学 来源: 题型:
【题目】为研究患肺癌与是否吸烟有关,某机构做了一次相关调查,制成如下图的![]() 列联表,其中数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的
列联表,其中数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的![]() ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为![]() .
.
患肺癌 | 不患肺癌 | 合计 | |
吸烟 | |||
不吸烟 | |||
总计 |
(1)若吸烟不患肺癌的有4人,现从患肺癌的人中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行调查,求这两人都是吸烟患肺癌的概率;
(2)若研究得到在犯错误概率不超过0.001的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)证明:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() .
.
(2)是否存在最大的整数![]() ,使得函数
,使得函数![]() 在其定义域上是增函数?若存在,求
在其定义域上是增函数?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一. 坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村中60户农民种植苹果、40户农民种植梨、20户农民种植草莓(每户仅扶持种植一种水果),为了更好地了解三种水果的种植与销售情况,现从该村随机选6户农民作为重点考察对象;
(1)用分层抽样的方法,应选取种植苹果多少户?
(2)在上述抽取的6户考察对象中随机选2户,求这2户种植水果恰好相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 上纵坐标为
上纵坐标为![]() 的点
的点![]() 到焦点的距离为2.
到焦点的距离为2.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)如图,![]() 为抛物线上三点,且线段
为抛物线上三点,且线段![]() 与
与![]() 轴交点的横坐标依次组成公差为1的等差数列,若
轴交点的横坐标依次组成公差为1的等差数列,若![]() 的面积是
的面积是![]() 面积的
面积的![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年元旦班级联欢晚会上,某班在联欢会上设计了一个摸球表演节目的游戏,在一个纸盒中装有1个红球,1个黄球,1个白球和1个黑球,这些球除颜色外完全相同,A同学不放回地每次摸出1个球,若摸到黑球则停止摸球,否则就要将纸盒中的球全部摸出才停止.规定摸到红球表演两个节目,摸到白球或黄球表演一个节目,摸到黑球不用表演节目.
(1)求A同学摸球三次后停止摸球的概率;
(2)记X为A同学摸球后表演节目的个数,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数. 设
为自然对数的底数. 设![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)若![]() 时,函数
时,函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的单调区间;
上的单调区间;
(Ⅲ)若![]() ,函数
,函数![]() 在区间
在区间![]() 内有零点,求
内有零点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com