
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.

(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]()
![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(I)见解析; (II)![]() ; (Ⅲ)答案见解析 .
; (Ⅲ)答案见解析 .
【解析】
(Ⅰ)由题意结合三角形中位线的性质和线面平行的判定定理即可证得题中的结论;
(Ⅱ)由题意建立空间直角坐标系,求得半平面的法向量,然后结合法向量可得二面角的余弦值;
(Ⅲ)假设存在满足题意的点![]() ,由题意结合点的坐标和向量垂直的充分必要条件得到关于
,由题意结合点的坐标和向量垂直的充分必要条件得到关于![]() 的方程,解方程即可确定
的方程,解方程即可确定![]() 的值.
的值.
(I)设![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
因为底面![]() 是矩形,所以
是矩形,所以![]() 为
为![]() 中点 .
中点 .
又因为![]() 为
为![]() 中点 , 所以
中点 , 所以![]() ∥
∥![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
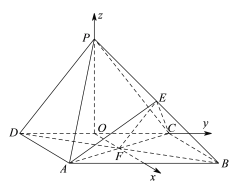
(II)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() .
.
因为底面![]() 为矩形,所以
为矩形,所以![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ∥
∥![]() ,所以
,所以![]() .
.
又因为平面PCD⊥平面ABCD,![]() 平面
平面![]() 平面PCD∩平面ABCD=CD.
平面PCD∩平面ABCD=CD.
所以PO⊥平面ABCD,
如图,建立空间直角坐标系![]() ,则
,则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
, ![]()
所以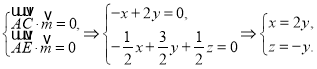
令![]() ,则
,则![]() ,所以
,所以![]() .
.
平面![]() 的法向量为
的法向量为![]() ,则
,则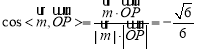 .
.
如图可知二面角![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)在棱![]() 上存在点
上存在点![]() , 使
, 使![]() .
.
设![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() ,解得
,解得![]() .
.
所以在棱![]() 上存在点
上存在点![]() ,使
,使![]() ,且
,且![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1(侧棱垂直于底面的棱柱)中,CA⊥CB,CA=CB=CC1=2,动点D在线段AB上.
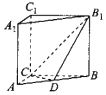
(1)求证:当点D为AB的中点时,平面B1CD⊥上平面ABB1A1;
(2)当AB=3AD时,求平面B1CD与平面BB1C1C所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为
且斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求![]() 的值;
的值;
(2)抛物线![]() 上一点
上一点![]() ,直线
,直线![]() (其中
(其中![]() )与抛物线
)与抛物线![]() 交于
交于![]() ,
,![]() 两个不同的点(均与点
两个不同的点(均与点![]() 不重合),设直线
不重合),设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() .动点
.动点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,其中
,其中![]() 为坐标原点.当线段
为坐标原点.当线段![]() 最长时,求直线
最长时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将红、黑、蓝、白5张纸牌(其中白纸牌有2张)随机分发给甲、乙、丙、丁4个人,每人至少分得1张,则下列两个事件为互斥事件的是( )
A. 事件“甲分得1张白牌”与事件“乙分得1张红牌”
B. 事件“甲分得1张红牌”与事件“乙分得1张蓝牌”
C. 事件“甲分得1张白牌”与事件“乙分得2张白牌”
D. 事件“甲分得2张白牌”与事件“乙分得1张黑牌”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点.
中点.
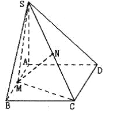
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)若![]() ,求实数
,求实数![]() 的值,使得直线
的值,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 相等”是“
相等”是“![]() 总相等”的
总相等”的

A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com