练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在直三棱柱中， 、分别为、的中点， ， .

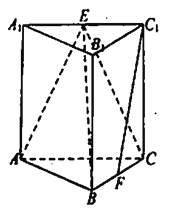
    （1）求证：平面平面；

    （2）若直线和平面所成角的正弦值等于，求二面角的平面角的正弦值.

    【答案】（1）见解析；（2）.

    【解析】试题分析：（1）要证面面垂直，先证线面垂直， 平面，再由面面垂直的判定得到面面垂直；（2）建系得到面的法向量和直线的方向向量，根据公式得到线面角的正弦值。.

    解析：

    （1）在直三棱柱中

    又

    平面， 平面，

    ∴平面

    又∵平面

    ∴平面平面.

    （2）由（1）可知

    以点为坐标原点， 为轴正方向， 为轴正方向， 为轴正方向，建立坐标系.设

    ， ， ， ， ， ， ，

    直线的方向向量，平面的法向量

    可知∴

    ， ，

    设平面的法向量

    ∴∴

    设平面的法向量

    ∴∴

    记二面角的平面角为

    ∴

    二面角的平面角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】学校艺术节对四件参赛作品只评一件一等奖，在评奖揭晓前，甲，乙，丙，丁四位同学对这四件参赛作品预测如下：

    甲说：“是或作品获得一等奖”； 乙说：“ 作品获得一等奖”；

    丙说：“ 两件作品未获得一等奖”； 丁说：“是作品获得一等奖”．

    评奖揭晓后，发现这四位同学中只有两位说的话是对的，则获得一等奖的作品是_________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形是边长为2的菱形，且，平面，，，点是线段上任意一点．

    (1)证明：平面平面；

    (2)若的最大值是，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数，下列判断正确的是（ ）

    A. 有最大值和最小值

    B. 的图象的对称中心为（）

    C. 在上存在单调递减区间

    D. 的图象可由的图象向左平移个单位而得

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校进行自主招生选拔，分笔试和面试两个阶段进行，规定分数不小于笔试成绩中位数的具有面试资格.现有1000余名学生参加了笔试考试，所有学生的成绩均在区间内，其频率分布直方图如图.

    （1）求获得面试资格应划定的最低分数线；

    （2）从笔试得分在区间的学生中，利用分层抽样的方法随机抽取7人，那么从得分在区间与各抽取多少人?

    （3）从（2）抽取的7人中，选出4人参加学校座谈交流，学校打算给这4人一定的物质奖励，若该生分数在给予300元物质奖励，若该生分数在给予500元物质奖励，用表示学校发的奖金数额，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】由于当前学生课业负担较重，造成青少年视力普遍下降，现从湖口中学随机抽取16名学生，经校医用视力表检查得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）如下：

    （1）指出这组数据的众数和中位数；

    （2）若视力测试结果不低于5.0则称为“好视力”，求校医从这16人中选取3人，至多有1人是“好视力”的概率；

    （3）以这16人的样本数据来估计整个学校的总体数据，若从该校（人数很多）任选3人，记表示抽到“好视力”学生的人数，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若，，求函数在处的切线方程；

    （2）若，且是函数的一个极值点，确定的单调区间；

    （3）若，且对任意，恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知鲜切花的质量等级按照花枝长度进行划分，划分标准如下表所示.

    花枝长度

    鲜花等级

    三级

    二级

    一级

    某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花，现从两个种植基地购进的鲜切花中分别随机抽取30个样品，测量花枝长度并进行等级评定，所抽取样品数据如图所示.

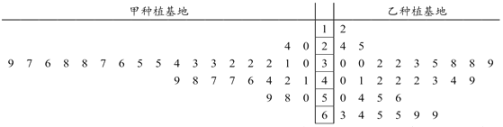
    （1）根据茎叶图比较两个种植基地鲜切花的花枝长度的平均值及分散程度(不要求计算具体值，给出结论即可)；

    （2）若从等级为三级的样品中随机选取2个进行新产品试加工，求选取的2个全部来自乙种植基地的概率；

    （3）根据该加工企业的加工和销售记录，了解到来自乙种植基地的鲜切花的加工产品的单件利润为4元；来自乙种植基地的鲜切花的加工产品的单件成本为10元，销售率(某等级产品的销量与产量的比值)及单价如下表所示.

    三级花加工产品

    二级花加工产品

    一级花加工产品

    销售率

    单价/(元/件)

    12

    16

    20

    由于鲜切花加工产品的保鲜特点，未售出的产品均可按原售价的50%处理完毕.用样本估计总体，如果仅从单件产品的利润的角度考虑，该鲜切花加工企业应该从哪个种植基地购进鲜切花？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】通过随机询问200名性别不同的大学生是否爱好踢毽子运动，计算得到统计量的观测值，参照附表，得到的正确结论是（ ）

    0.10

    0.05

    0.025

    2.706

    3.841

    5.024

    A.有97.5%以上的把握认为“爱好该项运动与性别有关”

    B.有97.5%以上的把握认为“爱好该项运动与性别无关”

    C.在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关”

    D.在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关”

    查看答案和解析>>

    同步练习册答案