
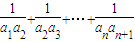 <
<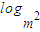 (m2-m)关于n∈N*恒成立,求正数m的范围;
(m2-m)关于n∈N*恒成立,求正数m的范围;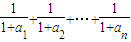 ,求证:4T2n≥n+2.
,求证:4T2n≥n+2.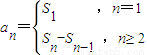 可得出an与an-1递推关系证明出{an}是等差数列;第2问因为第1问知{an}是等差数列,所以数列
可得出an与an-1递推关系证明出{an}是等差数列;第2问因为第1问知{an}是等差数列,所以数列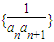 的前n项和可以用裂项法求出,然后根据数列的单调性和对数函数的单调性可以证明出该不等式.第3问先表达出Tn,然后在表达出
的前n项和可以用裂项法求出,然后根据数列的单调性和对数函数的单调性可以证明出该不等式.第3问先表达出Tn,然后在表达出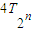 ,在构造
,在构造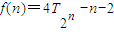 ,利用f(n)-f(n-1)结果的正、负来判断出单调性,从而可以证明出最后的结论.
,利用f(n)-f(n-1)结果的正、负来判断出单调性,从而可以证明出最后的结论.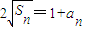 ,即4Sn=1+2an+an2 ①
,即4Sn=1+2an+an2 ①
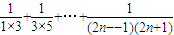
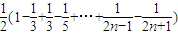
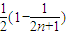
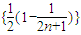 单调性知:
单调性知: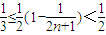
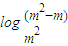
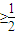 ,其中m>0且 m≠1
,其中m>0且 m≠1 =
=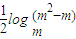
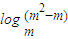 ≥1=logmm…③
≥1=logmm…③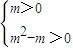 得:m>1
得:m>1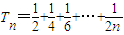
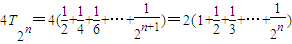
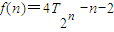
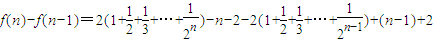
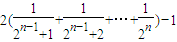
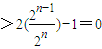
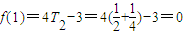
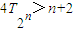 …14分
…14分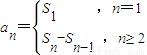 运用及等比数列的定义.第2问主要考查裂项法求和,关键要弄清裂项法“什么时候用?怎么用?”,难点在有根据数列的单调性得出
运用及等比数列的定义.第2问主要考查裂项法求和,关键要弄清裂项法“什么时候用?怎么用?”,难点在有根据数列的单调性得出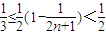 过渡到
过渡到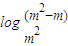
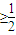 .第3问主要证明不等式的方法是作差,把差式构造成关于正整数的函数,利用后项减前项得出了单调性,体现了用函数思想解决数列问题的常规方法.总体来说综合性较强难度偏大.
.第3问主要证明不等式的方法是作差,把差式构造成关于正整数的函数,利用后项减前项得出了单调性,体现了用函数思想解决数列问题的常规方法.总体来说综合性较强难度偏大. 

科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| x+1 |
| 2 |
| ||
| a1 |
| ||
| a2 |
| ||
| a3 |
| ||
| an+1 |
| a1+an+1 |
| a1an+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a | 2 n |
| 1 |
| Sn |
| 17 |
| 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com