
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,与坐标轴分别交于A,B两点,且经过点Q(
,与坐标轴分别交于A,B两点,且经过点Q(![]() ,1).
,1).
(Ⅰ)求椭圆C的标准方程;
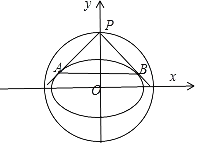
(Ⅱ)若P(m,n)为椭圆C外一动点,过点P作椭圆C的两条互相垂直的切线l1、l2,求动点P的轨迹方程,并求△ABP面积的最大值.
【答案】(Ⅰ)![]() 1;(Ⅱ)
1;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由离心率及椭圆过的点的坐标,及a,b,c之间的关系可得a,b的值,进而求出椭圆的方程;
(Ⅱ)过P的两条切线分斜率存在和不存在两种情况讨论,当斜率不存在时,直接由椭圆的方程可得切点A,B的坐标,当切线的斜率存在且不为0时,设过P的切线方程,与椭圆联立.由判别式等于0可得参数的关系,进而可得PA,PB的斜率之积,进而可得m,n之间的关系,即P的轨迹方程,显然切线斜率不存在时的点P也在轨迹方程上;因为PA,PB互相垂直,所以三角形PAB的面积为S△ABP![]() |PA||PB|
|PA||PB|![]() ,当且仅当|PA|=|PB|时取等号,此时得到点P的坐标求解.
,当且仅当|PA|=|PB|时取等号,此时得到点P的坐标求解.
(Ⅰ)由题意可得e![]() ,
,![]() 1,c2=a2﹣b2,解得a2=4,b2=2,
1,c2=a2﹣b2,解得a2=4,b2=2,
所以椭圆的方程为:![]() 1;
1;
(Ⅱ)设两个切点分别为A,B,①当两条切线中有一条斜率不存在时,
即A,B两点分别位于椭圆的长轴和短轴的端点,此时P的坐标为:(±2,±![]() ),
),
②当两条切线的斜率存在且不为0时,设过P的切线的方程为:y﹣n=k(x﹣m),
联立直线y﹣n=k(x﹣m)和椭圆的方程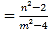 ,整理可得(1+2k2)x2﹣4k(km﹣n)x+2(km﹣n)2﹣4=0,
,整理可得(1+2k2)x2﹣4k(km﹣n)x+2(km﹣n)2﹣4=0,
由题意可得△=16k2(km﹣n)2﹣4(1+2k2)[2(km﹣n)2﹣4]=0,整理可得(m2﹣4)k2﹣2kmn+n2﹣2=0,所以k1k2![]() ,
,
设直线PA,PB的斜率分别为k1,k2,则k1k2![]() ,
,
而PA,PB互相垂直,所以![]() 1,
1,
即m2+n2=6,(m≠±2),
又因为P(±2,![]() )在m2+n2=6上,
)在m2+n2=6上,
所以点P在圆x2+y2=6上.
因为l1⊥l2,
所以span>S△ABP![]() |PA||PB|
|PA||PB|![]() ,当且仅当|PA|=|PB|时取等号,
,当且仅当|PA|=|PB|时取等号,
即P在椭圆的短轴所在的直线上时即P(0,![]() ),
),
由圆及椭圆的对称性设P(0,![]() ),则直线PA的斜率为1,可得直线PA的方程为:y=x
),则直线PA的斜率为1,可得直线PA的方程为:y=x![]() ,
,
代入椭圆的方程可得3x2+4![]() x+8=0,解得x
x+8=0,解得x![]() ,y
,y![]() ,即A(
,即A(![]() ,
,![]() ),
),
所以|PA|![]() ,所以AB2=2|PA|2
,所以AB2=2|PA|2![]() ,
,
所以(S△ABP)max![]() .
.


科目:高中数学 来源: 题型:
【题目】某小区楼顶成一种“楔体”形状,该“楔体”两端成对称结构,其内部为钢架结构(未画出全部钢架,如图1所示,俯视图如图2所示),底面![]() 是矩形,
是矩形,![]() 米,
米,![]() 米,屋脊
米,屋脊![]() 到底面
到底面![]() 的距离即楔体的高为1.5米,钢架所在的平面
的距离即楔体的高为1.5米,钢架所在的平面![]() 与
与![]() 垂直且与底面的交线为
垂直且与底面的交线为![]() ,
,![]() 米,
米,![]() 为立柱且O是
为立柱且O是![]() 的中点.
的中点.
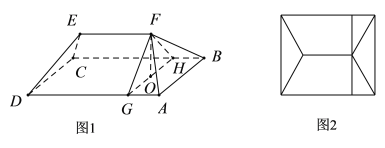
(1)求斜梁![]() 与底面
与底面![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求此模体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
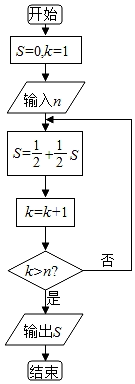
【题目】庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈(![]() ,
,![]() ),则输入的n的值为( )
),则输入的n的值为( )
A.7B.6C.5D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】干支纪年法是中国历法上自古以来就一直使用的纪年方法、干支是天干和地支的总称,甲、乙、丙、丁、戊、己、庚、辛、壬、癸为天干:子、丑、寅、卯、辰、已、午、未,申、西、戌、亥为地支.把十天干和十二地支依次相配,如甲对子、乙对丑、丙对寅、…癸对寅,其中天干比地支少两位,所以天干先循环,甲对戊、乙对亥、…接下来地支循环,丙对子、丁对丑、.,以此用来纪年,今年2020年是庚子年,那么中华人民共和国建国100周年即2049年是( )
A.戊辰年B.己巳年C.庚午年D.庚子年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,点
,点![]() 是
是![]() 上的不同于顶点的动点,
上的不同于顶点的动点,![]() 上在点
上在点![]() 处的切线
处的切线![]() 分别与
分别与![]() 轴轴交于点
轴轴交于点![]() 、
、![]() .若存在常数
.若存在常数![]() 满足对任意的点
满足对任意的点![]() 都有
都有![]() .
.
(Ⅰ)求实数![]() ,
,![]() 的值;
的值;
(Ⅱ)过点![]() 作
作![]() 的垂线与
的垂线与![]() 交于不同于
交于不同于![]() 的一点
的一点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρsin2θ-8cosθ=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系xOy.在直角坐标系中,倾斜角为α的直线l过点P(2,0).
(1)写出曲线C的直角坐标方程和直线l的参数方程;
(2)设点Q与点G的极坐标分别为![]() ,(2,π),若直线l经过点Q
,(2,π),若直线l经过点Q![]() ,且与曲线C相交于A,B两点,求△GAB的面积.
,且与曲线C相交于A,B两点,求△GAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 绕极点逆时针旋转
绕极点逆时针旋转![]() 后得到曲线
后得到曲线![]() .
.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() :
:![]() 与
与![]() ,
,![]() 分别相交于异于极点的
分别相交于异于极点的![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com