
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{3\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
分析 由已知中直线l的倾斜角可得其斜率,再由直线l经过点(0,-2),可得直线的点斜式方程,可得直线在两坐标轴上的截距,代入三角形面积公式可得答案.
解答 解:因为直线l的倾斜角的大小为60°,
故其斜率为$\sqrt{3}$,
又直线l经过点(0,-2),所以其方程为y-(-2)=$\sqrt{3}$x,
即$\sqrt{3}$x-y-2=0,
由直线l的方程知它在x轴、y轴上的截距分别是$\frac{2}{\sqrt{3}}$、-2,
所以直线l与两坐标轴围成三角形的面积S=$\frac{1}{2}•\frac{2}{\sqrt{3}}•2$=$\frac{2\sqrt{3}}{3}$,
故选:D.
点评 本题考查直线的方程,其中根据直线l经过点(0,-2),结合直线的斜率,求出直线方程是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,x2>0”的否定是“?x0∈R,x02≤0” | |
| B. | “?x0∈R,x02<0”的否定是“?x∈R,x2<0” | |
| C. | “?θ0∈R,sinθ0+cosθ0<1”的否定是“?θ∈R,sinθ+cosθ≥1” | |
| D. | “?θ∈R,sinθ≤1”的否定是?θ0∈R,sinθ0>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 90° | B. | 60° | C. | 30° | D. | 0° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3] | B. | [-1,3] | C. | (3,+∞) | D. | (-1,0)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
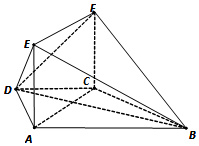 在梯形ABCD中AB∥CD,AD=CD=CB=2,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=2.
在梯形ABCD中AB∥CD,AD=CD=CB=2,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com