
【题目】公交车的数量太多容易造成资源浪费,太少又难以满足乘客的需求,为了合理布置车辆,公交公司在2路车的乘客中随机调查了50名乘客,经整理,他们候车时间(单位:![]() )的茎叶图如下:
)的茎叶图如下:

(Ⅰ)将候车时间分为![]() 八组,作出相应的频率分布直方图;
八组,作出相应的频率分布直方图;
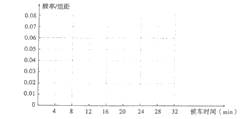
(Ⅱ)若公交公司将2路车发车时间调整为每隔15![]() 发一趟车,那么上述样本点将发生变化(例如候车时间为9
发一趟车,那么上述样本点将发生变化(例如候车时间为9![]() 的不变,候车时间为17
的不变,候车时间为17![]() 的变为2
的变为2![]() ),现从2路车的乘客中任取5人,设其中候车时间不超过10
),现从2路车的乘客中任取5人,设其中候车时间不超过10![]() 的乘客人数为
的乘客人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)根据茎叶图可得落在各组内的频数,求得频率后可得![]() 的值,根据所得数据可得频率分布直方图.(Ⅱ)由题意得候车时间中不超过10分钟的数据共有34个,根据古典概型概率公式可得所求概率为0.68.
的值,根据所得数据可得频率分布直方图.(Ⅱ)由题意得候车时间中不超过10分钟的数据共有34个,根据古典概型概率公式可得所求概率为0.68.
试题解析:
(Ⅰ)由茎叶图可得落入分组区间![]() 内的频数依次为4、4、10、12、8、6、4、2,
内的频数依次为4、4、10、12、8、6、4、2,
于是可得各组分组区间相应的![]() 的值依次为0.02、0.02、0.05、0.06、0.04、0.03、0.02、
的值依次为0.02、0.02、0.05、0.06、0.04、0.03、0.02、
0.01,
依此画出频率分布直方图如下图所示.
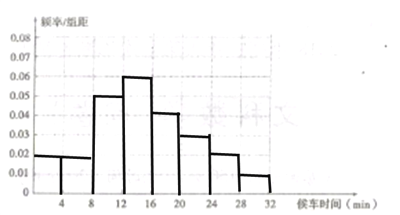
(Ⅱ)调整为间隔15分钟发一趟车之后,候车时间原本不超过10分钟的数据就有14个,发生了变化的候车时间中不超过10分钟的数据又增加了20个,共计34个.
所以候车时间不超过10分钟的频率为![]() ,
,
由此估计一名乘客候车时间不超过10分钟的概率为0.68.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】几千年的沧桑沉淀,凝练了西樵山的美,清幽秀丽的自然风光,文化底蕴厚重的旅游,古朴自然的民俗风情.自明清以来,文人雅士,群贤毕至,旅人游子,纷至沓来,使秀美的西樵山成为名嗓南粤的旅游热点.如图,游客从某旅游景区的景点![]() 处下山至
处下山至![]() 处有两种路径,一种是从
处有两种路径,一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 乘景区观光车到
乘景区观光车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从
匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从![]() 乘观光车到
乘观光车到![]() ,在
,在![]() 处停留20分钟后,再从
处停留20分钟后,再从![]() 匀速步行到
匀速步行到![]() .假设观光车匀速直线运行的速度为250米/分钟,山路
.假设观光车匀速直线运行的速度为250米/分钟,山路![]() 长为2340米,经测量,
长为2340米,经测量,![]() ,
,![]() .
.
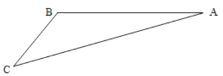
(1)求观光车路线![]() 的长;
的长;
(2)问乙出发多少分钟后,乙在观光车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且Sn=2n-1(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log4an+1,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
B. α,β∈R,使cos(α+β)=cosα+cosβ
C. 向量a=(2,1),b=(-1,0),则a在b的方向上的投影为2
D. “|x|≤1”是“x≤1”的既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=![]() 与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则
与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则![]() (xi+yi)=( )
(xi+yi)=( )
A. 0 B. m
C. 2m D. 4m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
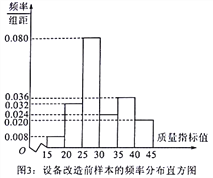
表1:设备改造后样本的频数分布表

(1)完成下面的![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;

(2)根据图3和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件售价240元;质量指标值落在
内的定为一等品,每件售价240元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
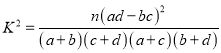
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() 。
。
(1)若点![]() 在圆
在圆![]() 内,求
内,求![]() 的取值范围;
的取值范围;
(2)若过点![]() 的圆
的圆![]() 的切线只有一条,求切线的方程;
的切线只有一条,求切线的方程;
(3)当![]() 时,过点
时,过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程。
的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com