
【题目】在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() .
.
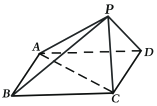
(1)证明:面![]() ⊥面
⊥面![]() ;
;
(2)若![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)要证面面垂直,一般先证线面垂直,设AC与BD交点为O,则PO⊥BD,而正方形中AC⊥BD,于是可证得结论.
(2)由线面角的定义可得![]() ,以A为坐标原点,
,以A为坐标原点,![]() 为x,y轴的正方向建立空间直角坐标系,然后写出各点坐标,求出面BPC和面DPC的法向量,再由法向量的夹角的余弦值得二面角的余弦.
为x,y轴的正方向建立空间直角坐标系,然后写出各点坐标,求出面BPC和面DPC的法向量,再由法向量的夹角的余弦值得二面角的余弦.
(1)证明:连接AC,BD交点为O,∵四边形ABCD为正方形,∴![]()
∵![]() ,
,![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]()
又![]() ,∴
,∴![]() .
.
(2)∵![]() ,过点P做
,过点P做![]() ,垂足为E
,垂足为E
∴![]() ∵PA与底面ABCD所成的角为
∵PA与底面ABCD所成的角为![]() ,∴
,∴![]() ,
,
又![]() ,设
,设![]() ,则
,则
![]()
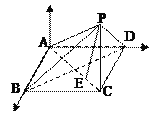
如图所示,以A为坐标原点,![]() 为x,y轴的正方向建立空间直角坐标系
为x,y轴的正方向建立空间直角坐标系![]()
![]()
设面![]() 法向量为
法向量为,
![]()
 ,∴
,∴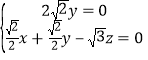 ,
,
![]() ,∴
,∴![]()
同理![]() 的法向量
的法向量![]() ,
,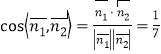
∴求二面角![]() 的余弦值
的余弦值![]()


科目:高中数学 来源: 题型:
【题目】如图所示,使用纸板可以折叠粘贴制作一个形状为正六棱柱形状的花型锁盒盖的纸盒. 
(1)求该纸盒的容积;
(2)如果有一张长为60cm,宽为40cm的矩形纸板,则利用这张纸板最多可以制作多少个这样的纸盒(纸盒必须用一张纸板制成).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程![]() ,其中a,b是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率.
,其中a,b是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率.
(1)若随机数a,b∈{1,2,3,4,5,6};
(2)若a是从区间[0,5]中任取的一个数,b是从区间[2,4]中任取的一个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程![]() ,其中a,b是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率.
,其中a,b是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率.
(1)若随机数a,b∈{1,2,3,4,5,6};
(2)若a是从区间[0,5]中任取的一个数,b是从区间[2,4]中任取的一个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,则该算法的功能是( ) 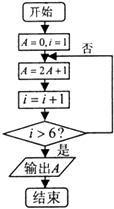
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() =1(a>b>0)的焦点F1 , F2 , 过右焦点F2的直线l与C相交于P、Q两点,若△PQF1的周长为短轴长的2
=1(a>b>0)的焦点F1 , F2 , 过右焦点F2的直线l与C相交于P、Q两点,若△PQF1的周长为短轴长的2 ![]() 倍.
倍.
(1)求C的离心率;
(2)设l的斜率为1,在C上是否存在一点M,使得 ![]() ?若存在,求出点M的坐标;若不存在,说明理由.
?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,且保费与上一年度车辆发生道路交通事故的情况相联系.发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表 | ||
浮动因素 | 浮动比率 | |
A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 | A1 | A2 | A3 | A4 | A5 | A6 |
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5 000元,一辆非事故车盈利10 000元.且各种投保类型的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有6辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆车,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(x+ ![]() )cosx.
)cosx.
(1)若0≤x≤ ![]() ,求函数f(x)的值域;
,求函数f(x)的值域;
(2)设△ABC的三个内角A,B,C所对的边分别为a,b,c,若A为锐角且f(A)= ![]() ,b=2,c=3,求cos(A﹣B)的值.
,b=2,c=3,求cos(A﹣B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(
(α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(![]() )=2
)=2![]() .
.
(Ⅰ)求曲线C和直线l在该直角坐标系下的普通方程;
(Ⅱ)动点A在曲线C上,动点B在直线l上,定点P的坐标为(﹣2,2),求|PB|+|AB|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com