
【题目】设函数![]() (
(![]() 为常数,
为常数,![]() 是自然对数的底数).
是自然对数的底数).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 内存在两个极值点,求
内存在两个极值点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调递减区间为
的单调递减区间为![]() 单调递增区间为
单调递增区间为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)求出导函数,根据导函数的正负性,求出函数的单调区间;
(Ⅱ)函数f(x)在(0,2)内存在两个极值点,等价于它的导函数f′(x)在(0,2)内有两个不同的零点.
试题解析:(1).函数![]() 的定义域为
的定义域为![]()
![]()
由![]() 可得
可得![]() ,
,
所以当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
所以![]() 的单调递减区间为
的单调递减区间为![]() 单调递增区间为
单调递增区间为![]() .
.
(2).由1知,![]() 时,函数
时,函数![]() 在
在![]() 内单调递减,
内单调递减,
故![]() 在
在![]() 内不存在极值点;
内不存在极值点;
当![]() 时,设函数
时,设函数![]() ,
,![]() ,
,
因为![]() ,
,
当![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
故![]() 在
在![]() 内不存在两个极值点;
内不存在两个极值点;
当![]() 时,得
时,得![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
所以函数![]() 的最小值为
的最小值为![]() ,
,
函数![]() 在
在![]() 内存在两个极值点,
内存在两个极值点,
当且仅当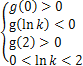 ,解得
,解得![]() .
.
综上所述,函数![]() 在
在![]() 内存在两个极值点时,
内存在两个极值点时,![]() 的取值范围为
的取值范围为![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,函数
时,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求实数b的取值范围.
成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在其定义域内为增函数,求
在其定义域内为增函数,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两条不重合的直线,
是两条不重合的直线, ![]() 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题:
①若![]() ,
, ![]() ,则
,则![]() ;
;
②若![]() ,
, ![]() ,
, ![]() ,则
,则![]() ;
;
③若![]() ,
, ![]() ,
, ![]() ,则
,则![]() ;
;
④当![]() ,且
,且![]() 时,若
时,若![]() ,则
,则![]() .
.
其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】读下列所给程序,依据程序画出程序框图,并说明其功能.
INPUT “输入三个正数a,b,c=”;a,b,c
IF a+b>c AND a+c>b AND b+c>a THEN
p=(a+b+c)/2
S=SQR(p*(p-a)*(p-b)*(p-c))
PRINT “三角形的面积S=”S
ELSE
PRINT “构不成三角形”
END IF
END.
查看答案和解析>>
科目:高中数学 来源: 题型:
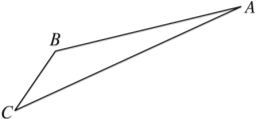
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于一点
相交于一点![]() ,
, ![]() ,将
,将![]() 沿着
沿着![]() 折起得
折起得![]() ,连接
,连接![]() .
.
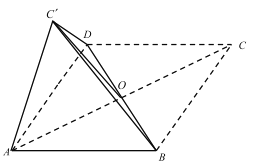
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在平面
在平面![]() 上的投影恰好是
上的投影恰好是![]() 的重心,求直线
的重心,求直线![]() 与底面
与底面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极小值;
的极小值;
(3)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com