
����С������12�֣�
ijѧУ����֪ʶ��������һ��ѡ�ι�����A��B��C��D�ĸ����⣬�������£�
ÿλ�μ��Ƿ����ij�ʼ�־�Ϊ10�֣��������A��B��C��D�ֱ��1�֡�2�֡�3�֡�6�֣������һ���2�֣�
ÿ�ش�һ�⣬�Ƿ�����ʾ�ۼƷ��������ۼƷ���С��8��ʱ�������������̭���֣����ۼƷ������ڻ����14��ʱ�����������������һ�֣����������⣬�ۼƷ����Բ���14��ʱ�������������̭���֣�
ÿλ�μ��߰�����A��B��C��D˳������ֱ�����������
�����ͬѧ������A��B��C��D�ش���ȷ�ĸ�������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ���Ҹ���ش���ȷ����֮��û��Ӱ�졣
���Ҹ���ش���ȷ����֮��û��Ӱ�졣
�������ͬѧ�ܽ�����һ�ֵĸ��ʣ�
�����æα�ʾ��ͬѧ���ִ������ʱ����ĸ�������εķֲ��к���ѧ�������Ρ�
��С����Ҫ������ɢ����������ķֲ��к���ѧ��������������¼��������¼��ĸ��ʺ���ⷽ���������ø���֪ʶ���ʵ�������������
�⣺��A��B��C��D�ֱ�Ϊ��һ�����������ĸ����⣬��MI��I=1,2,3,4����ʾ��ͬѧ��i������ش���ȷ����N��i=1,2,3,4)��ʾ��ͬѧ��i������ش������Mi��Ni�Ƕ����¼���i=1,2,3,4��.�������
P(MI)=![]()
![]() ,P(M2)=
,P(M2)= ![]() ��P(M3)=
��P(M3)=![]() P(M4)=
P(M4)=![]() ��
��
���� p��N1��=![]() , P(N2)=
, P(N2)= ![]() , P(N3)=
, P(N3)=![]() , P(N4)=
, P(N4)=![]() .��������������������
.��������������������
(��)�ǡ���ͬѧ�ܽ�����һ�֡�Ϊ�¼�Q,
��Q=M1M2M3+ N1M2M3M4+ M1N2M3M4+ M1M2N3M4+ N1M2N3M4
����ÿ�����������������
P��Q��=P��M1M2M3+ N1M2M3M4+ M1N2M3M4+ M1M2N3M4+ N1M2N3M4��
=P��M1M2M3��+ P��N1M2M3M4��+ P��M1N2M3M4��+ P��M1M2N3M4��+ P��N1M2N3M4��
= P��M1��P��M2��P��M3��+ P��N1��P��M2��P��M3��P��M4��+ P��M1��P��N2��P��M3��P��M4��+ P��M1��P��M2��P��N3��P��M4��+ P��N1��P��M2��P��N3��P��M4��
=![]() +
+![]()
=![]()
(��)�����⣬��������εĿ���ȡֵΪ��2,3,4��
����ÿ�������������������� P����=2��= P��N1 N2��= P��N1��P��N2��=![]()
P����=3��= P��M1M2M3��+ P��M1N2N3��
= P��M1�� P��M2��P��M3��+ P��M1�� P��N2��P��N3��
=![]()
=![]()
P����=4��=1- P����=2��- P����=3��
=1-![]() -
-![]()
=![]()
��� ��������εķֲ���Ϊ
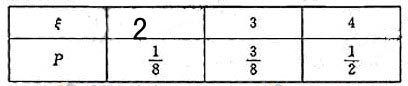
����E��=2![]()


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������12�֣���֪����![]() ����
����![]() ������
������![]() �����ֵ����Сֵ������
�����ֵ����Сֵ������![]() ���ڶ������ϵĵ�������.
���ڶ������ϵĵ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��2009���Ͼ��ģ�����С������12�֣�
Ϊ��������������ij�о����½�һ���ص㹤�̣��ֱ�Ϊ������ʩ���̡��������̺Ͳ�ҵ���蹤�����࣬�������������Ŀ�ĸ����ֱ�ռ������![]() ��
��![]() ��
��![]() .����3�����˶����ش�����ѡһ����Ŀ���뽨��.��
.����3�����˶����ش�����ѡһ����Ŀ���뽨��.��
��I������ѡ�����Ŀ���������ͬ�ĸ��ʣ� w.w.w.k.s.5.u.c.o.m ![]()
![]()
��II��������1��ѡ�����Ŀ�����������̵ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����С������12�֣�
ij��Ӫ��ҵ����A��B���ֲ�Ʒ�������г������Ԥ�⣬A��Ʒ��������Ͷ�ʳ����ȣ����ϵ��ͼ1��B��Ʒ��������Ͷ�ʵ�����ƽ���������ȣ����ϵ��ͼ2��
��ע��������Ͷ�ʵ�λ����Ԫ��
��1���ֱ�A��B���ֲ�Ʒ�������ʾΪͶ�ʵĺ�������д�����ǵĺ�����ϵʽ.��2������ҵ�ѳO��10��Ԫ�ʽ𣬲�ȫ��Ͷ�뵽A��B���ֲ�Ʒ���������ʣ�����������10��ԪͶ�ʣ�����ʹ��ҵ�������������������Ϊ������Ԫ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com