
分析 求出向量$\overrightarrow{m}$,通过向量的数量积求解向量$\overrightarrow{m}$与$\overrightarrow{n}$的夹角.
解答 解:向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(9,12),$\overrightarrow{n}$=(7,1)且$\overrightarrow{m}$=2$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,-4).
向量$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为θ,
cosθ=$\frac{\overrightarrow{m}•\overrightarrow{n}}{\left|\overrightarrow{m}\right|\left|\overrightarrow{n}\right|}$=$\frac{-21-4}{\sqrt{(-3)^{2}+({-4)}^{2}}×\sqrt{{7}^{2}+{1}^{2}}}$=$-\frac{\sqrt{2}}{2}$,
θ=135°.
向量$\overrightarrow{m}$与$\overrightarrow{n}$的夹角的大小为135°.
点评 本题考查平面向量的数量积的应用,向量的夹角的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
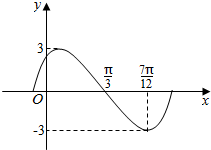 函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象的一部分如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com