【题目】已知函数
， 
.
（1）若曲线
在
处的切线与直线
垂直，求实数
的值；
（2）设
，若对任意两个不等的正数
，都有
恒成立，求实数
的取值范围；
（3）若
上存在一点
，使得
成立，求实数
的取值范围.
【答案】（1）
（2）
（3）
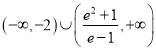
【解析】试题分析：（1）先根据导数几何意义得
，解得实数
的值；（2）设
，构造函数
，则转化为
在
上为增函数，即得
在
上恒成立，参变分离得
，最后根据二次函数最值求实数
的取值范围；（3）先化简不等式，并构造函数
，求导数，按导函数零点与定义区间大小关系讨论函数单调性，根据单调性确定函数最小值，根据最小值小于零解得实数
的取值范围.
试题解析：解：（1）由
，得
.
由题意， 
，所以
.
（2）
.
因为对任意两个不等的正数
，都有
恒成立，设
，则
即
恒成立.
问题等价于函数
，
即
在
上为增函数，
所以
在
上恒成立.即
在
上恒成立.
所以
，即实数
的取值范围是
.
（3）不等式
等价于
，整理得
.构造函数
，
由题意知，在
上存在一点
，使得
.
.
因为
，所以
，令
，得
.
①当
，即
时， 
在
上单调递增.只需
，解得
.
②当
即
时， 
在
处取最小值.
令
即
，可得
.
令
，即
，不等式
可化为
.
因为
，所以不等式左端大于1，右端小于等于1，所以不等式不能成立.
③当
，即
时， 
在
上单调递减，只需
，解得
.
综上所述，实数
的取值范围是
.
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
(a>b>0)的离心率为
，短轴长为2.直线l：y＝kx＋m与椭圆C交于M，N两点，又l与直线
， 
分别交于A，B两点，其中点A在第一象限，点B在第二象限，且△OAB的面积为2(O为坐标原点).
(1)求椭圆C的方程；
(2)求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，一智能扫地机器人在
处发现位于它正西方向的
处和北偏东30°方向上的
处分别有需要清扫的垃圾，红外线感应测量发现机器人到的距离比到的距离少0.4米，于是选择沿
路线清扫，已知智能扫地机器人的直线行走速度为0.2
，忽略机器人吸入垃圾及在处旋转所用时间，10秒钟完成了清扫任务．
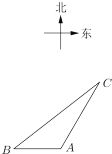
（1）、两处垃圾的距离是多少？
（2）智能扫地机器人此次清扫行走路线的夹角
的正弦值是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着人口老龄化的到来，我国的劳动力人口在不断减少，“延迟退休”已经成为人们越来越关注的话题，为了解公众对“延迟退休”的态度，某校课外研究性学习小组在某社区随机抽取了50人进行调查，将调查情况进行整理后制成下表：
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在［25,30),[55,60）的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人，进行跟踪调查．
（I）求年龄在［25,30）的被调查者中选取的2人都赞成“延迟退休”的概率；
（II）若选中的4人中，不赞成“延迟退休”的人数为
，求随机变量
的分布列和数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，圆
的普通方程为
. 在以坐标原点为极点，
轴正半轴为极轴的极坐标系中，直线
的极坐标方程为
.
（Ⅰ） 写出圆 的参数方程和直线的直角坐标方程；
（ Ⅱ ） 设直线 与轴和
轴的交点分别为
，
为圆上的任意一点，求
的取值范围.
【答案】(1)
;
.
(2)
.
【解析】【试题分析】(I)利用圆心和半径,写出圆的参数方程,将圆的极坐标方程展开后化简得直角坐标方程.(II)求得
两点的坐标, 设点
，代入向量,利用三角函数的值域来求得取值范围.
【试题解析】
（Ⅰ）圆的参数方程为
（
为参数）.
直线的直角坐标方程为
.
（Ⅱ）由直线
的方程可得点
，点
.
设点，则 
.
.
由（Ⅰ）知，则 
.
因为
，所以
.
【题型】解答题
【结束】
23
【题目】选修4-5：不等式选讲
已知函数
， 
.
（Ⅰ）若对于任意
， 
都满足
，求
的值；
（Ⅱ）若存在
，使得
成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年2月9-25日，第23届冬奥会在韩国平昌举行.4年后，第24届冬奥会将在中国北京和张家口举行.为了宣传冬奥会，某大学在平昌冬奥会开幕后的第二天，从全校学生中随机抽取了120名学生，对是否收看平昌冬奥会开幕式情况进行了问卷调查，统计数据如下：
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根据上表说明，能否有
的把握认为，收看开幕式与性别有关？
(Ⅱ)现从参与问卷调查且收看了开幕式的学生中，采用按性别分层抽样的方法选取8人，参加2022年北京冬奥会志愿者宣传活动.
(ⅰ)问男、女学生各选取多少人？
(ⅱ)若从这8人中随机选取2人到校广播站开展冬奥会及冰雪项目宣传介绍，求恰好选到一名男生一名女生的概率P.
附：
，其中
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂家具车间造
、
型两类桌子，每张桌子需木工和漆工梁道工序完成.已知木工做一张、型型桌子分别需要1小时和2小时，漆工油漆一张、型型桌子分别需要3小时和1小时；又知木工、漆工每天工作分别不得超过8小时和9小时，而工厂造一张、型型桌子分别获利润2千元和3千元.
(1)列出满足生产条件的数学关系式，并画出可行域；
(2)怎样分配生产任务才能使每天的利润最大，最大利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
