练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】中国古代算书《孙子算经》中有一著名的问题“物不知数”如图1，原题为：今有物，不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？后来，南宋数学家秦九韶在其著作《数学九章》中对此类问题的解法做了系统的论述，并称之为“大衍求一术”，如图2程序框图的算法思路源于“大衍求一术”执行该程序框图，若输入的a，b分别为20，17，则输出的c=（ ）

    A.1
    B.6
    C.7
    D.11

    【答案】C
    【解析】解：模拟执行程序运行过程，如下；
    a=20，b=17，r=3，c=1，m=0，n=1，满足r≠1；
    a=17，b=3，r=2，q=5，m=1，n=1，c=6，满足r≠1；
    a=3，b=2，r=1，q=1，m=1，n=6，c=7，满足r=1；
    输出c=7．
    故选：C．
    模拟执行程序运行过程，即可得出程序运行后输出的c值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设y=f(t)是某港口水的深度y(米)关于时间t(小时)的函数，其中.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：

    t

    0

    3

    6

    9

    12

    15

    18

    21

    24

    y

    12

    15.1

    12.1

    9.1

    12

    14.9

    11.9

    9

    12.1

    经长期观察，函数y=f(t)的图象可以近似地看成函数的图象.⑴求的解析式；⑵设水深不小于米时，轮船才能进出港口。某轮船在一昼夜内要进港口靠岸办事，然后再出港。问该轮船最多能在港口停靠多长时间？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四面体ABCD的顶点都在球O表面上，且AB=BC=AC=2 ，DA=DB=DC=2，过AD作相互垂直的平面α、β，若平面α、β截球O所得截面分别为圆M、N，则（ ）
    A.MN的长度是定值
    B.MN长度的最小值是2
    C.圆M面积的最小值是2π
    D.圆M、N的面积和是定值8π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】当时，函数的值域是_________.

    【答案】[－1，2]

    【解析】：f（x）=sinx+cosx=2（sinx+cosx）=2sin（x+），

    ∵﹣≤x≤，

    ∴﹣≤x+≤，

    ∴﹣≤sin（x+）≤1，

    ∴函数f（x）的值域为[﹣1，2]，

    故答案为：[﹣1，2]．

    【题型】填空题
    【结束】
    15

    【题目】若点O在内，且满足，设为的面积， 为的面积，则＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直三棱柱ABC﹣A1B1C1中，∠ABC=90°，E、F分别为A1C1、B1C1的中点，D为棱CC1上任一点．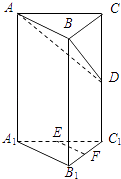

    （Ⅰ）求证：直线EF∥平面ABD；
    （Ⅱ）求证：平面ABD⊥平面BCC1B1 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量，，设函数．

    （1）若函数的图象关于直线对称，且时，求函数的单调增区间；

    （2）在（1）的条件下，当时，函数有且只有一个零点，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝6cos2＋sinωx－3(ω>0)在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．

    (1)求ω的值及函数f(x)的值域；

    (2)若f(x0)＝，且x0∈(－，)，求f(x0＋1)的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣1|﹣|2x+1|的最大值为m
    （1）作函数f（x）的图象
    （2）若a2+b2+2c2=m，求ab+2bc的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】运行如图所示的程序框图，则输出结果为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案