
【题目】若![]() 、
、![]() 两点分别在函数
两点分别在函数![]() 与
与![]() 的图像上,且关于直线
的图像上,且关于直线![]() 对称,则称
对称,则称![]() 、
、![]() 是
是![]() 与
与![]() 的一对“伴点”(
的一对“伴点”(![]() 、
、![]() 与
与![]() 、
、![]() 视为相同的一对).已知
视为相同的一对).已知 ,
,![]() ,若
,若![]() 与
与![]() 存在两对“伴点”,则实数
存在两对“伴点”,则实数![]() 的取值范围为________.
的取值范围为________.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=2,点M为A1C1的中点,点N为AB1上一动点.若点N为AB1的中点且CM⊥MN,求二面角MCNA的正弦值.
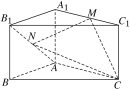
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实验中学在教工活动中心举办了一场台球比赛,为了节约时间比赛采取“3局2胜制”.现有甲、乙二人,已知每局甲胜的概率为0.6,乙胜的概率为0.4.求:
(1)这场比赛甲获胜的概率;
(2)这场比赛乙所胜局数的数学期望.
(3)这场比赛在甲获得比赛胜利的条件下,乙有一局获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AC⊥BC,O为AB中点,且DC⊥平面ABC,DC∥BE.已知AC=BC=DC=BE=2.
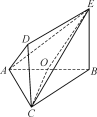
(1)求直线AD与CE所成角;
(2)求二面角O-CE-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: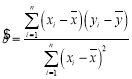 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市场上有一种新型的强力洗衣粉,特点是去污速度快,已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中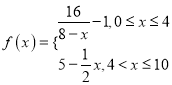 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
(1)若只投放一次4个单位的洗衣液,则有效去污时间可能达几分钟?
(2)若先投放2个单位的洗衣液,6分钟后投放![]() 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: ![]() 取
取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝建国70周年,校园文化节举行有奖答题活动,现有A,B两种题型,从A类题型中抽取1道,从B类题型中抽取2道回答,答对3道题获新华书店面值为15元的图书代金券,答对2道题获面值为10元的图书代金券,答对1道题获面值为5元的图书代金券,没有答对获面值为1元的图书代金券(作为鼓励).甲同学参加此活动答对A类题的概率为![]() ,答对B类题的概率为
,答对B类题的概率为![]() .
.
(Ⅰ)求甲答对1道题的概率;
(Ⅱ)设甲参加一次活动所获图书代金券的面值为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com