
【题目】已知p:x2﹣6x+5≤0,q:x2﹣2x+1﹣m2≤0(m>0).
(1)若m=2,且p∧q为真,求实数x的取值范围;
(2)若p是q充分不必要条件,求实数m的取值范围.
【答案】
(1)解:由x2﹣6x+5≤0,得1≤x≤5,
∴p:1≤x≤5;
当m=2时,q:﹣1≤x≤3.
若p∧q为真,p,q同时为真命题.,
则 ![]() ,即1≤x≤3
,即1≤x≤3
(2)解:由x2﹣2x+1﹣m2≤0,得q:1﹣m≤x≤1+m.
∵p是q充分不必要条件,
∴[1,5][1﹣m,1+m],
∴ 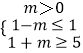 ,解得m≥4.
,解得m≥4.
∴实数m的取值范围为m≥4
【解析】(1)分别求解一元二次不等式化简p,q,然后利用p∧q为真,取交集求得实数x的取值范围;(2)求解一元二次不等式化简q,结合p是q充分不必要条件,可得[1,5][1﹣m,1+m],转化为关于m的不等式组得答案.
【考点精析】掌握复合命题的真假是解答本题的根本,需要知道“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,C上一点(3,m)到焦点的距离为5.
(1)求C的方程;
(2)过F作直线l,交C于A、B两点,若线段AB中点的纵坐标为﹣1,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2 ![]() ,M为AB的中点.
,M为AB的中点. 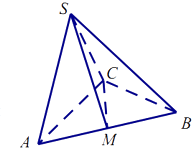
(1)求证:AC⊥SB;
(2)求二面角S﹣CM﹣A的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣x,g(x)=xlnx.
(1)求函数f(x)的最大值;
(2)设0<a<b,证明0<g(a)+g(b)﹣2g( ![]() )<(b﹣a)ln2.
)<(b﹣a)ln2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( ) 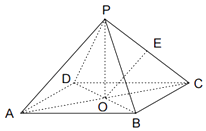
A.30°
B.60°
C.45°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的奇函数f(x)= ![]() ,其中h(x)是指数函数,且h(2)=4.
,其中h(x)是指数函数,且h(2)=4.
(1)求函数f(x)的解析式;
(2)求不等式f(2x﹣1)>f(x+1)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ex﹣ ![]() (x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣∞, ![]() )
)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从椭圆 ![]() 上一点P向x轴作垂线,垂足恰为左焦点F1 , 又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且
上一点P向x轴作垂线,垂足恰为左焦点F1 , 又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且 ![]() . (Ⅰ) 求椭圆的方程;
. (Ⅰ) 求椭圆的方程;
(Ⅱ) 若M是椭圆上的动点,点N(4,2),求线段MN中点Q的轨迹方程.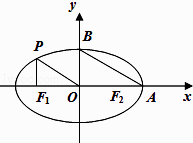
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com