
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,BC∥AD,AB⊥BC,∠ADC=45°,PA⊥平面ABCD,AB=AP=1,AD=3.
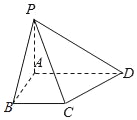
(1)求异面直线PB与CD所成角的大小;
(2)求点D到平面PBC的距离.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)建立空间直角坐标系,利用向量法求异面直线PB与CD所成角大小.
(2)求出平面PBC的一个法向量,利用向量法的距离公式求点D到平面PBC的距离.
(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立如图所示空间直角坐标系,
则P(0,0,1),B(1,0,0),C(1,2,0)D(0,3,0),
∴![]() =(1,0,﹣1),
=(1,0,﹣1),![]() =(﹣1,1,0),
=(﹣1,1,0),
设异面直线PB与CD所成角为θ,
则cosθ=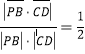 ,
,
所以异面直线PB与CD所成角大小为![]() .
.
(2)设平面PBC的一个法向量为![]() =(x,y,z),
=(x,y,z),
![]() =(1,0,﹣1),
=(1,0,﹣1),![]() =(0,2,0),
=(0,2,0),![]() =(﹣1,1,0),
=(﹣1,1,0),
则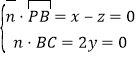 ,取x=1,得
,取x=1,得![]() =(1,0,1),
=(1,0,1),
∴点D到平面PBC的距离d=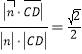 .
.


科目:高中数学 来源: 题型:
【题目】如图所示,近日我渔船编队在岛![]() 周围海域作业,在岛
周围海域作业,在岛![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与![]() 相距31海里的
相距31海里的![]() 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛![]() 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达![]() 处,此时观测站测得
处,此时观测站测得![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问海警船再向前航行多少分钟方可到岛![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地沿某条公路行驶一共200公里,遇到红灯个数的概率如下表所示:
红灯个数 | 0 | 1 | 2 | 3 | 4 | 5 | 6个及6个以上 |
概率 | 0.02 | 0.1 |
| 0.35 | 0.2 | 0.1 | 0.03 |
(1)求表中字母![]() 的值;
的值;
(2)求至少遇到4个红灯的概率;
(3)求至多遇到5个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业对设备进行技术升级改造,为了检验改造效果,现从设备改造后生产的大量产品中抽取了100件产品作为样本,检测一项质量指标值,统计整理为如图所示的频率分布直方图:
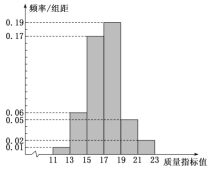
(1)估计该企业所生产产品的质量指标的平均数和中位数(中位数保留一位小数);
(2)若产品的质量指标在![]() 内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在
内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在![]() 范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆M:![]()
![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且内切于圆
的离心率互为倒数,且内切于圆![]() 。
。
(1)求椭圆M的方程;
(2)已知![]() ,
,![]() 是椭圆M的下焦点,在椭圆M上是否存在点P,使
是椭圆M的下焦点,在椭圆M上是否存在点P,使![]() 的周长最大?若存在,请求出
的周长最大?若存在,请求出![]() 周长的最大值,并求此时
周长的最大值,并求此时![]() 的面积;若不存在,请说明理由。
的面积;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列{an},记T={x|x=aj﹣ai,i<j},若数列{an}满足:“存在t∈T,使得只要am﹣ak=t(m,k∈N*,m>k),必有am+1﹣ak+1=t”,则称数列具有性质P(t).
(1)若数列{an}满足![]() ,判断数列{an}是否具有性质P(2)?是否具有性质P(4)?说明理由;
,判断数列{an}是否具有性质P(2)?是否具有性质P(4)?说明理由;
(2)求证:“T是有限集”是“数列{an}具有性质P(0)”的必要不充分条件;
(3)已知{bn}是各项均为正整数的数列,且{bn}既具有性质P(2),又具有性质P(5),求证:存在正整数N,使得aN,aN+1,aN+2,…,aN+K,…是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com