【答案】
分析:(Ⅰ)由题设知D
n内的整点在直线x=1和x=2上.记直线y=-mx+3m为l,l与直线x=1和x=2的交点的纵坐标分别为y
1、y
2,由y
1=2n,y
2=n,知a
n=3n(n∈N*),再用数学归纳法证明.
(Ⅱ)先求得

,所以

.因为对一切n∈N
*,T
n>m恒成立,所以m<T
n的最小值,从而可求.
解答:
解:(Ⅰ)当n=1时,D
1为Rt△OAB
1的内部包括斜边,这时a
1=3,
当n=2时,D
2为Rt△OAB
2的内部包括斜边,这时a
2=3,
当n=3时,D
3为Rt△OAB
3的内部包括斜边,这时a
3=9
由此可猜想a
n=3n
下面用数学归纳法证明:
(1)当n=1时,猜想显然成立.
(2)假设当n=k时,猜想成立,即a
k=3k
如图,平面区域D
k为Rt△OAB
k内部包括斜边、平面区域D
k+1为Rt△△OAB
k+1内部包括斜边,∵平面区域D
k+1比平面区域D
k多3个整点,(7分)
即当n=k+1时,a
k+1=3k+3=3(k+1),这就是说当n=k+1时,猜想也成立,
由(1)、(2)知a
n=3n对一切n∈N
*都成立.(8分)
(Ⅱ)∵a
n=3n,∴数列{a
n}是首项为3,公差为3的等差数列,
∴

.∴

,∴

∵对一切n∈N
*,T
n>m恒成立,∴m<T
n的最小值.
∵

在[1,+∞)上为增函数∴T
n的最小值为

,∴

,满足
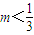
的自然数为0,
∴满足题设的自然数m存在,其值为0.(14分)
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用和不等式的应用.

 (n∈N*)
(n∈N*) }的前项和Tn,
}的前项和Tn,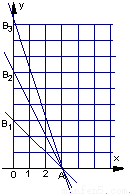
 ,所以
,所以 .因为对一切n∈N*,Tn>m恒成立,所以m<Tn的最小值,从而可求.
.因为对一切n∈N*,Tn>m恒成立,所以m<Tn的最小值,从而可求. 解:(Ⅰ)当n=1时,D1为Rt△OAB1的内部包括斜边,这时a1=3,
解:(Ⅰ)当n=1时,D1为Rt△OAB1的内部包括斜边,这时a1=3, .∴
.∴ ,∴
,∴
 在[1,+∞)上为增函数∴Tn的最小值为
在[1,+∞)上为增函数∴Tn的最小值为 ,∴
,∴ ,满足
,满足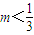 的自然数为0,
的自然数为0,

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案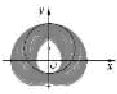 如图,阴影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )
如图,阴影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )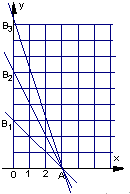 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组