
【题目】已知函数f(x)=4cosωxsin(ωx+ ![]() )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间[0, ![]() ]上的单调性;
]上的单调性;
(3)当x∈[0, ![]() ]时,关于x的方程f(x)=a 恰有两个不同的解,求实数a的取值范围.
]时,关于x的方程f(x)=a 恰有两个不同的解,求实数a的取值范围.
【答案】
(1)解:f(x)=4cosωxsin(ωx+ ![]() )
)
=2 ![]() sinωxcosωx+2
sinωxcosωx+2 ![]() cos2ωx,
cos2ωx,
= ![]() (sin 2ωx+cos 2ωx)+
(sin 2ωx+cos 2ωx)+ ![]() ,
,
=2sin(2ωx+ ![]() )+
)+ ![]() ,
,
因为f(x)的最小正周期为π,且ω>0,从而有 ![]() =π,
=π,
故ω=1
(2)解:由(1)知,f(x)=2sin(2x+ ![]() )+
)+ ![]() .若0≤x≤
.若0≤x≤ ![]() ,则
,则 ![]() ≤2x+
≤2x+ ![]() ≤
≤ ![]() .
.
当 ![]() ≤2x+
≤2x+ ![]() ≤
≤ ![]() ,即0≤x≤
,即0≤x≤ ![]() 时,f(x)单调递增;
时,f(x)单调递增;
当 ![]() ≤2x+
≤2x+ ![]() ≤
≤ ![]() ,即
,即 ![]() ≤x≤
≤x≤ ![]() 时,f(x)单调递减.
时,f(x)单调递减.
综上可知,f(x)在区间[0, ![]() ]上单调递增,在区间[
]上单调递增,在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
(3)解:x∈[0, ![]() ]时,关于x的方程f(x)=a 恰有两个不同的解,
]时,关于x的方程f(x)=a 恰有两个不同的解,
即y=a与函数在[0, ![]() ]上,与f(x)=2sin(2x+
]上,与f(x)=2sin(2x+ ![]() )+
)+ ![]() 由两个交点,
由两个交点,
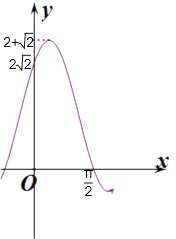
由函数图象可知:a∈[2 ![]() ,2+
,2+ ![]() ),
),
实数a的取值范围[2 ![]() ,2+
,2+ ![]() )
)
【解析】(1)由两角和的正弦公式及辅助角公式化简f(x),根据周期公式即可求得ω的值;(2)由(1)求得f(x)的解析式,根据正弦函数图象及性质即可判断函数区间[0, ![]() ]上的单调性;(3)由题意可知y=a与函数在[0,
]上的单调性;(3)由题意可知y=a与函数在[0, ![]() ]上,与f(x)=2sin(2x+
]上,与f(x)=2sin(2x+ ![]() )+
)+ ![]() 由两个交点,根据函数图象即可求得实数a的取值范围.
由两个交点,根据函数图象即可求得实数a的取值范围.


科目:高中数学 来源: 题型:
【题目】某微信群中有甲、乙、丙、丁、戊五个人玩抢红包游戏,现有4个红包,每人最多抢一个,且红包被全部抢完,4个红包中有2个6元,1个8元,1个10元(红包中金额相同视为相同红包),则甲、乙都抢到红包的情况有( )
A. 18种 B. 24种 C. 36种 D. 48种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x
cos2x
(1)求f(x)的最小正周期和单调增区间;
(2)若将f(x)的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图象,当x∈[ ![]() ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d>0.设{an}的前n项和为Sn,a1=1,S2·S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 在圆
在圆![]() :
: ![]() 上运动,定点
上运动,定点![]() ,线段
,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 的交点为
的交点为![]() .
.
(Ⅰ)求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() ,
, ![]() 分别交轨迹
分别交轨迹![]() 于
于![]() ,
, ![]() 两点和
两点和![]() ,
, ![]() 两点,且
两点,且![]() .证明:过
.证明:过![]() 和
和![]() 中点的直线过定点.
中点的直线过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定两个命题,P:对任意实数x都有ax2+ax+1>0恒成立;Q:关于x的方程x2﹣x+a=0有实数根;如果P与Q中有且仅有一个为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC是斜三角形,内角A、B、C所对的边的长分别为a、b、c.若csinA= ![]() acosC.
acosC.
(1)求角C;
(2)若c= ![]() ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com