���
�⣺��1����x
1��x
2��[0��+�ޣ�����x
1��x
2��
g��x
1��-g��x
2��=-x
+x
=��x
2+x
1����x
2-x
1����
��x
1��x
2��[0��+�ޣ���x
1��x
2��
��x
2+x
1��0��x
2-x
1��0��
�ࣨx
2+x
1����x
2-x
1����0��
��g��x
1��-g��x
2����0��
g��x
1����g��x
2����
����g��x��=-x
2��x��[0��+�ޣ������䶨�������ǵ����ݼ�������٣�
���躯��g��x����M�����������[a��b]ʹ��f��x����[a��b]�ϵ���Сֵ��a�����ֵ��b��
���ɢٿ�֪����g��x��=-x
2��x��[0��+�ޣ������䶨�������ǵ����ݼ���
����g��x������[a��b]���ǵ����ݼ���
��
���������Ľⲻ���ڣ�
����費����������g��x��=-x
2��x��[0��+�ޣ��������ڼ���M��
��2��֤��������f��x��=3log
2x������Ϊ{x|x��0}��
��x
1��x
2�ʣ�0��+�ޣ�����x
1��x
2��
f��x
1��-f��x
2��=3log
2x
1-3log
2x
2=3log
2��
��x
1��x
2�ʣ�0��+�ޣ�����x
1��x
2��
��
��1��
��3log
2��0��
��f��x
1��-f��x
2����0��
��f��x
1����f��x
2����
����f��x��=3log
2x���䶨�������ǵ���������
����f��x����M���ں���f��x���Ķ������ڴ��ڱ�����[a��b]��ʹ��f��x����[a��b]�ϵ���Сֵ��a�����ֵ��b��
��
����g��x��=2
-x������g��1����0��g��3����0��g��9����0��g��12����0������ͼ
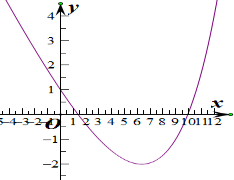
����1��a��3��9��b��12��ʹ��g��a��=0��g��b��=0��
Ҳ���Ǻ���f��x���Ķ������ڴ��ڱ�����[a��b]ʹ��f��x����[a��b]�ϵ���Сֵ��a�����ֵ��b
���ϣ�����f��x��=3log
2x���ڼ���M��֤��
��3��m=0ʱ������f��x��=0��������M����m��0
f��x���Ķ�����ΪR������f��
x��=
=
��m��0ʱ��f��
x���ֱ��ڣ�-�ޣ�0���ͣ�0��+�ޣ��ϵ�����������?x��0��f��x����0��?x��0��f��x����0����f��x����R�ϵ���������
ͬ����֤��m��0ʱ��f��x����R�ϵ����ݼ��������ڶ�������Ϊ����������
������f��
x��=
���ڼ���M��
���ں���f��x���Ķ�����R�ڴ��ڱ�����[a��b]��ʹ��f��x����[a��b]�ϵ���Сֵ��a�����ֵ��b��
��������
=x����������ʵ����Ҳ����x��0��
=1����m=1+|x|��1
���ϣ�m��1




