
【题目】![]() 满足约束条件
满足约束条件 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为( )
的值为( )
A. ![]() 或
或![]() B. 2或
B. 2或![]() C. 2 D.
C. 2 D. ![]() 或
或![]()
【答案】D
【解析】分析:由约束条件作出可行域,将![]() ,化为
,化为![]() ,z相当于
,z相当于![]() 的纵截距,由几何意义可得。
的纵截距,由几何意义可得。
详解:由题中约束条件作可行域如下图所示:
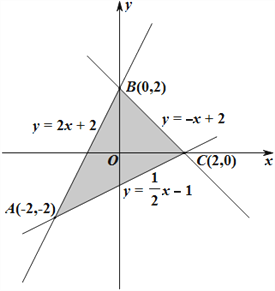
将![]() 化为
化为![]() ,即直线
,即直线![]() 的纵截距取得最大值时的最优解不唯一。
的纵截距取得最大值时的最优解不唯一。
当![]() 时,直线
时,直线![]() 经过点A(-2,-2)时纵截距最大,此时最优解仅有一个,故不符合题意;
经过点A(-2,-2)时纵截距最大,此时最优解仅有一个,故不符合题意;
当a=2时,直线![]() 与
与![]() 重合时纵截距最大,此时最优解不唯一,故符合题意;
重合时纵截距最大,此时最优解不唯一,故符合题意;
当![]() 时,直线
时,直线![]() 经过点B(0,2)时纵截距最大,此时最优解仅有一个,故不符合题意;
经过点B(0,2)时纵截距最大,此时最优解仅有一个,故不符合题意;
当a=-1时,直线![]() 与y=-x+2重合时纵截距最大,此时最优解不唯一,故符合题意;
与y=-x+2重合时纵截距最大,此时最优解不唯一,故符合题意;
当a<-1时,直线![]() 经过点C(2,0)时纵截距最大,此时最优解仅有一个,故不符合题意。
经过点C(2,0)时纵截距最大,此时最优解仅有一个,故不符合题意。
综上,当a=2或a=-1时最优解不唯一,符合题意。
故本题正确答案为D。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2018年3月山东省高考改革实施方案发布:2020年夏季高考开始全省高考考生总成绩将由语文、数学、外语三门统一高考成绩和学生自主选择的普通高中学业水平等级性考试科目的成绩共同构成.省教育厅为了解正就读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见.右面是根据样本的调查结果绘制的等高条形图.

(Ⅰ)请根据已知条件与等高条形图完成下面的![]() 列联表:
列联表:
赞成 | 不赞成 | 合计 | |
城镇居民 | |||
农村居民 | |||
合计 |
(Ⅱ)试判断我们是否有95%的把握认为“赞成高考改革方案与城乡户口有关”?.
【附】![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C满足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+ ![]() ,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
A.bc(b+c)>8
B.ab(a+b)>16 ![]()
C.6≤abc≤12
D.12≤abc≤24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记max{x,y}= ![]() ,min{x,y}=
,min{x,y}= ![]() ,设
,设 ![]() ,
, ![]() 为平面向量,则( )
为平面向量,则( )
A.min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}≤min{|
|}≤min{| ![]() |,|
|,| ![]() |}
|}
B.min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}≥min{|
|}≥min{| ![]() |,|
|,| ![]() |}
|}
C.max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}≤|
|2}≤| ![]() |2+|
|2+| ![]() |2
|2
D.max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}≥|
|2}≥| ![]() |2
|2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设每一架飞机的引擎在飞行中出现故障率为![]() ,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机也可成功飞行,要使4引擎飞机比2引擎飞机更安全,则
,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机也可成功飞行,要使4引擎飞机比2引擎飞机更安全,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= ![]() .
. 
(1)证明:DE⊥平面ACD;
(2)求二面角B﹣AD﹣E的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com