
°æƒø°ø2020ƒÍ≥ı£¨–¬π⁄∑Œ—◊“þ«ÈœÆª˜»´π˙£¨∂‘»À√Ò…˙√¸∞≤»´∫Õ…˙≤˙…˙ªÓ‘Ï≥…—œ÷ÿ”∞œÏ.‘⁄µ≥∫Õ’˛∏Æ«ø”–¡¶µƒøπ“þ¡Ïµºœ¬£¨Œ“π˙øÿ÷∆◊°“þ«È∫Û£¨“ª∑Ω√Ê∑¿÷πæ≥Õ‚“þ«È ‰»Î£¨¡Ì“ª∑Ω√Ê÷≤Ω∏¥π§∏¥≤˙£¨ºı«·æ≠º√œ¬Ωµ∂‘∆Û“µ∫Õ√Ò÷⁄¥¯¿¥µƒÀ ß.Œ™ΩµµÕ“þ«È”∞œÏ£¨ƒ≥≥ߺ“ƒ‚‘⁄2020ƒÍ柖–ƒ≥≤˙∆∑µƒ¥Ÿœ˙ªÓ∂Ø£¨æ≠µ˜≤È≤‚À„£¨∏√≤˙∆∑µƒƒÍœ˙ €¡ø£®º¥∏√≥ßµƒƒÍ≤˙¡ø£©![]() ÕÚº˛”΃ͥŸœ˙∑—”√
ÕÚº˛”΃ͥŸœ˙∑—”√![]() ÕÚ‘™£®
ÕÚ‘™£®![]() £©¬˙◊„
£©¬˙◊„![]() £®
£®![]() Œ™≥£ ˝£©£¨»Áπ˚≤ª∏„¥Ÿœ˙ªÓ∂Ø£¨‘Ú∏√≤˙∆∑µƒƒÍœ˙ €¡ø÷ªƒÐ «2ÕÚº˛.“—÷™…˙≤˙∏√≤˙∆∑µƒπÃ∂®Õ∂»ÎŒ™8ÕÚ‘™£¨√ø…˙≤˙“ªÕÚº˛∏√≤˙∆∑–Ë“™‘ŸÕ∂»Î16ÕÚ‘™£¨≥ߺ“Ω´√øº˛≤˙∆∑µƒœ˙ €º€∏Ò∂®Œ™√øº˛≤˙∆∑ƒÍ∆Ωæ˘≥…±æµƒ1.5±∂£®¥À¥¶√øº˛≤˙∆∑ƒÍ∆Ωæ˘≥…±æ∞¥
Œ™≥£ ˝£©£¨»Áπ˚≤ª∏„¥Ÿœ˙ªÓ∂Ø£¨‘Ú∏√≤˙∆∑µƒƒÍœ˙ €¡ø÷ªƒÐ «2ÕÚº˛.“—÷™…˙≤˙∏√≤˙∆∑µƒπÃ∂®Õ∂»ÎŒ™8ÕÚ‘™£¨√ø…˙≤˙“ªÕÚº˛∏√≤˙∆∑–Ë“™‘ŸÕ∂»Î16ÕÚ‘™£¨≥ߺ“Ω´√øº˛≤˙∆∑µƒœ˙ €º€∏Ò∂®Œ™√øº˛≤˙∆∑ƒÍ∆Ωæ˘≥…±æµƒ1.5±∂£®¥À¥¶√øº˛≤˙∆∑ƒÍ∆Ωæ˘≥…±æ∞¥![]() ‘™¿¥º∆À„£©
‘™¿¥º∆À„£©
£®1£©Ω´2020ƒÍ∏√≤˙∆∑µƒ¿˚»Û![]() ÕÚ‘™±Ì 挙ƒÍ¥Ÿœ˙∑—”√
ÕÚ‘™±Ì 挙ƒÍ¥Ÿœ˙∑—”√![]() ÕÚ‘™µƒ∫Ø ˝£ª
ÕÚ‘™µƒ∫Ø ˝£ª
£®2£©∏√≥ߺ“2020ƒÍµƒ¥Ÿœ˙∑—”√Õ∂»Î∂ý…ŸÕÚ‘™ ±£¨≥ߺ“µƒ¿˚»Û◊Ó¥Û£ø
°æ¥∞∏°ø£®1£©![]() £ª
£ª
£®2£©2018ƒÍµƒ¥Ÿœ˙∑—”√Õ∂»Î3ÕÚ‘™ ±£¨≥ߺ“µƒ¿˚»Û◊Ó¥ÛŒ™29ÕÚ‘™.
°æΩ‚Œˆ°ø
£®1£©∏˘æð“‚![]() ±£¨
±£¨![]() £¨«Û≥ˆ
£¨«Û≥ˆ![]() £¨Ω¯“ª≤Ω«Û≥ˆœ˙ €º€∏Ò
£¨Ω¯“ª≤Ω«Û≥ˆœ˙ €º€∏Ò![]() £¨”…¿˚»Û
£¨”…¿˚»Û![]() œ˙ €∂Ó
œ˙ €∂Ó![]() πÃ∂®≥…±æ
πÃ∂®≥…±æ![]() ‘ŸÕ∂»Î≥…±æ
‘ŸÕ∂»Î≥…±æ![]() ¥Ÿœ˙∑—£¨º¥ø…«ÛΩ‚.
¥Ÿœ˙∑—£¨º¥ø…«ÛΩ‚.
£®2£©”…£®1£©![]() £¨¿˚”√ª˘±æ≤ªµ» Ωº¥ø…«ÛΩ‚.
£¨¿˚”√ª˘±æ≤ªµ» Ωº¥ø…«ÛΩ‚.
£®1£©”…“‚÷™£¨µ±![]() ±£¨
±£¨![]() £®ÕÚº˛£©£¨
£®ÕÚº˛£©£¨
‘Ú![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨![]() .
.
À˘“‘√øº˛≤˙∆∑µƒœ˙ €º€∏ÒŒ™![]() £®‘™£©£¨
£®‘™£©£¨
![]() 2018ƒÍµƒ¿˚»Û
2018ƒÍµƒ¿˚»Û![]() .
.
£®2£©![]() µ±
µ±![]() ±£¨
±£¨![]() £¨
£¨
![]() £¨µ±«“Ωˆµ±
£¨µ±«“Ωˆµ±![]() ±µ»∫≈≥…¡¢.
±µ»∫≈≥…¡¢.
![]() £¨
£¨
µ±«“Ωˆµ±![]() £¨º¥
£¨º¥![]() ÕÚ‘™ ±£¨
ÕÚ‘™ ±£¨![]() £®ÕÚ‘™£©.
£®ÕÚ‘™£©.
π ∏√≥ߺ“2018ƒÍµƒ¥Ÿœ˙∑—”√Õ∂»Î3ÕÚ‘™ ±£¨≥ߺ“µƒ¿˚»Û◊Ó¥ÛŒ™29ÕÚ‘™.


 ª™∂´ ¶¥Û∞Ê“ªøŒ“ª¡∑œµ¡–¥∞∏
ª™∂´ ¶¥Û∞Ê“ªøŒ“ª¡∑œµ¡–¥∞∏ √œΩ®∆Ω√˚–£øºæÌœµ¡–¥∞∏
√œΩ®∆Ω√˚–£øºæÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f(x)=2lnx-ax2,»Ù¶¡£¨¶¬∂º Ù”⁄«¯º‰[1,4]£¨«“¶¬-¶¡=1£¨f(¶¡)=f(¶¬),‘Ú µ ˝aµƒ»°÷µ∑∂Œß «________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ˝‘≠µ„µƒ“ªÃı÷±œþ”ÎÕ÷‘≤![]() =1£®a£æb£æ0£©Ωª”⁄A£¨B¡Ωµ„£¨“‘œþ∂ŒABŒ™÷±æ∂µƒ‘≤π˝∏√Õ÷‘≤µƒ”“Ωπµ„F2£¨»Ù°œABF2° [
=1£®a£æb£æ0£©Ωª”⁄A£¨B¡Ωµ„£¨“‘œþ∂ŒABŒ™÷±æ∂µƒ‘≤π˝∏√Õ÷‘≤µƒ”“Ωπµ„F2£¨»Ù°œABF2° [![]() ]£¨‘Ú∏√Õ÷‘≤¿Î–ƒ¬ µƒ»°÷µ∑∂ŒßŒ™£®°°°°£©
]£¨‘Ú∏√Õ÷‘≤¿Î–ƒ¬ µƒ»°÷µ∑∂ŒßŒ™£®°°°°£©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() «π´≤Ó≤ªŒ™¡„µƒµ»≤Ó ˝¡–£¨¬˙◊„
«π´≤Ó≤ªŒ™¡„µƒµ»≤Ó ˝¡–£¨¬˙◊„![]() £¨«“
£¨«“![]() °¢
°¢![]() °¢
°¢![]() ≥…µ»±» ˝¡–.
≥…µ»±» ˝¡–.
£®1£©«Û ˝¡–![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
£®2£©…Ë ˝¡–![]() ¬˙◊„
¬˙◊„![]() £¨«Û ˝¡–
£¨«Û ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ
œÓ∫Õ![]() .
.
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©…˵»≤Ó ˝¡–![]() µƒπ´≤ÓŒ™
µƒπ´≤ÓŒ™![]() £¨”…a3=7£¨«“
£¨”…a3=7£¨«“![]() °¢
°¢![]() °¢
°¢![]() ≥…µ»±» ˝¡–£Æø…µ√
≥…µ»±» ˝¡–£Æø…µ√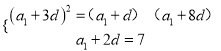 £¨Ω‚÷Ƶ√º¥ø…µ√≥ˆ ˝¡–
£¨Ω‚÷Ƶ√º¥ø…µ√≥ˆ ˝¡–![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
2£©”…£®1£©µ√![]() £¨‘Ú
£¨‘Ú![]() £¨”…¡—œÓœýœ˚∑®ø…«Û ˝¡–
£¨”…¡—œÓœýœ˚∑®ø…«Û ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ
œÓ∫Õ![]() .
.
‘Ã‚Ω‚Œˆ£∫£®1£©…Ë ˝¡–![]() µƒπ´≤ÓŒ™
µƒπ´≤ÓŒ™![]() £¨«“
£¨«“![]() ”…“‚µ√
”…“‚µ√![]() £¨
£¨
º¥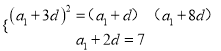 £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
À˘“‘ ˝¡–![]() µƒÕ®œÓπ´ Ω
µƒÕ®œÓπ´ Ω![]() .
.
£®2£©”…£®1£©µ√![]()
![]() £¨
£¨
![]()
![]() .
.
°æ–հøΩ‚¥Ã‚
°æΩ· ¯°ø
18
°æƒø°øÀƒ¿‚◊∂![]() µƒµ◊√Ê
µƒµ◊√Ê![]() Œ™÷±Ω«Ã𖌣¨
Œ™÷±Ω«Ã𖌣¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() Œ™’˝»˝Ω«–Œ.
Œ™’˝»˝Ω«–Œ.
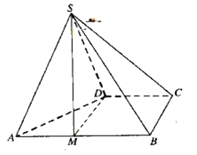
£®1£©µ„![]() Œ™¿‚
Œ™¿‚![]() …œ“ªµ„£¨»Ù
…œ“ªµ„£¨»Ù![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨![]() £¨«Û µ ˝
£¨«Û µ ˝![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©«Ûµ„BµΩ∆Ω√ÊSADµƒæý¿Î.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°∂÷–ª™»À√Òπ≤∫Õπ˙µ¿¬∑ΩªÕ®∞≤»´∑®°∑µ⁄47ÃıµƒœýπÿπÊ∂®£∫ª˙∂Ø≥µ––æ≠»À––µ¿ ±£¨”¶µ±ºıÀŸ¬˝––£ª”ˆ––»À’˝‘⁄Õ®π˝»À––µ¿£¨”¶µ±Õ£≥µ»√––£¨À◊≥∆°∞¿Ò»√∞þ¬Ìœþ°±£¨ °∂÷–ª™»À√Òπ≤∫Õπ˙µ¿¬∑ΩªÕ®∞≤»´∑®°∑µ⁄90ÃıπÊ∂®£∫∂‘≤ª¿Ò»√––»Àµƒºð ª‘±¥¶“‘ø€3∑÷£¨∑£øÓ50‘™µƒ¥¶∑£.œ¬±Ì «ƒ≥ –“ª÷˜∏…¬∑ø⁄ºýøÿ…˱∏À˘◊•≈ƒµƒ5∏ˆ‘¬ƒ⁄ºð ª‘±°∞¿Ò»√∞þ¬Ìœþ°±––Œ™Õ≥º∆ ˝æð£∫
‘¬∑ð | 1 | 2 | 3 | 4 | 5 |
Œ•’¬ºð ª‘±»À ˝ | 120 | 105 | 100 | 90 | 85 |
£®1£©«Î¿˚”√À˘∏¯ ˝æð«ÛŒ•’¬»À ˝![]() ”Α¬∑ð
”Α¬∑ð![]() ÷ƺ‰µƒªÿπÈ÷±œþ∑Ω≥Ã
÷ƺ‰µƒªÿπÈ÷±œþ∑Ω≥Ã![]() £ª
£ª
£®2£©‘§≤‚∏√¬∑ø⁄9‘¬∑ðµƒ≤ª°∞¿Ò»√∞þ¬Ìœþ°±Œ•’¬ºð ª‘±»À ˝.
≤Œøºπ´ Ω£∫ 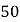 £¨
£¨ ![]() .
.
≤Œøº ˝æð£∫ ![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷±Ω«◊¯±ÍœµxOy÷–£¨“—÷™MN «‘≤C£∫(x©Å2)2+(y©Å3)2=2µƒ“ªÃıœ“£¨«“CM°ÕCN£¨P «MNµƒ÷–µ„.µ±œ“MN‘⁄‘≤C…œ‘À∂Ø ±£¨÷±œþl£∫x©Åy©Å5=0…œ◊Хʑ⁄¡Ωµ„A£¨B£¨ πµ√![]() ∫„≥…¡¢£¨‘Úœþ∂ŒAB≥§∂»µƒ◊Ó–°÷µ «_____.
∫„≥…¡¢£¨‘Úœþ∂ŒAB≥§∂»µƒ◊Ó–°÷µ «_____.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ù∂®“‘⁄R…œµƒ≈º∫Ø ˝![]() ¬˙◊„
¬˙◊„![]() £¨«“
£¨«“![]() ±,
±,![]() £¨‘Ú∫Ø ˝
£¨‘Ú∫Ø ˝![]() µƒ¡„µ„∏ˆ ˝ «( )
µƒ¡„µ„∏ˆ ˝ «( )
A. 6∏ˆB. 8∏ˆC. 2∏ˆD. 4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë![]() «¡ΩÃı≤ªÕ¨µƒ÷±œþ£¨
«¡ΩÃı≤ªÕ¨µƒ÷±œþ£¨ ![]() «¡Ω∏ˆ≤ªÕ¨µƒ∆Ω√Ê£¨‘Úœ¬¡–√¸Ã‚÷–’˝»∑µƒ «£® £©
«¡Ω∏ˆ≤ªÕ¨µƒ∆Ω√Ê£¨‘Úœ¬¡–√¸Ã‚÷–’˝»∑µƒ «£® £©
A. »Ù![]() £¨
£¨ ![]() £¨‘Ú
£¨‘Ú![]()
B. »Ù![]() ,
, ![]() ,‘Ú
,‘Ú![]()
C. »Ù![]() £¨
£¨ ![]() ,
, ![]() £¨‘Ú
£¨‘Ú![]()
D. »Ù![]() £¨«“
£¨«“![]() £¨µ„
£¨µ„![]() £¨÷±œþ
£¨÷±œþ![]() £¨‘Ú
£¨‘Ú![]()
°æ¥∞∏°øC
°æΩ‚Œˆ°øA. »Ù![]() £¨
£¨ ![]() £¨‘Ú
£¨‘Ú![]() ªÚ
ªÚ![]() £ª
£ª
B. »Ù![]() ,
, ![]() ,‘Ú
,‘Ú![]() ŒÞΩªµ„£¨º¥∆Ω––ªÚ“Ï√Ê£ª
ŒÞΩªµ„£¨º¥∆Ω––ªÚ“Ï√Ê£ª
C. »Ù![]() £¨
£¨ ![]() ,
, ![]() £¨π˝
£¨π˝![]() ◊˜∆Ω√Ê”Î
◊˜∆Ω√Ê”Î![]() ∑÷±Ωª”⁄÷±œþs,t,‘Ú
∑÷±Ωª”⁄÷±œþs,t,‘Ú![]() ,
, ![]() ,À˘“‘
,À˘“‘![]() t,‘Ÿ∏˘æðœþ√Ê∆Ω––≈–∂®∂®¿Ìµ√
t,‘Ÿ∏˘æðœþ√Ê∆Ω––≈–∂®∂®¿Ìµ√![]() £¨“ÚŒ™
£¨“ÚŒ™![]() £¨
£¨ ![]() ,À˘“‘
,À˘“‘![]() ,º¥
,º¥![]()
D. »Ù![]() £¨«“
£¨«“![]() £¨µ„
£¨µ„![]() £¨÷±œþ
£¨÷±œþ![]() £¨µ±B‘⁄∆Ω√Ê
£¨µ±B‘⁄∆Ω√Ê![]() ƒ⁄ ±≤≈”–
ƒ⁄ ±≤≈”–![]() ,
,
◊€…œ—°C.
°æ–հøµ•—°Ã‚
°æΩ· ¯°ø
11
°æƒø°øº◊°¢““°¢±˚°¢∂°ÀƒŒªÕ¨—ß≤Œº”±»»¸£¨÷ª”–∆‰÷–»˝ŒªªÒΩ±.º◊Àµ£∫°∞““ªÚ±˚Œ¥ªÒΩ±°±£ª““Àµ£∫°∞º◊°¢±˚∂ºªÒΩ±°±£ª±˚Àµ£∫°∞Œ“Œ¥ªÒΩ±°±£ª∂°Àµ£∫°∞““ªÒΩ±°±.ÀƒŒªÕ¨—ßµƒª∞«°”–¡Ωæ‰ «∂‘µƒ£¨‘Ú£® £©
A. º◊∫Õ““≤ªø…ƒÐÕ¨ ±ªÒΩ± B. ±˚∫Õ∂°≤ªø…ƒÐÕ¨ ±ªÒΩ±
C. ““∫Õ∂°≤ªø…ƒÐÕ¨ ±ªÒΩ± D. ∂°∫Õº◊≤ªø…ƒÐÕ¨ ±ªÒΩ±
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬Õº «ƒ≥ °¥”1‘¬21»’÷¡2‘¬24»’µƒ–¬π⁄∑Œ—◊√ø»’–¬‘ˆ»∑’Ô≤°¿˝±‰ªØ«˙œþÕº.

»Ù∏√ °¥”1‘¬21»’÷¡2‘¬24»’µƒ–¬π⁄∑Œ—◊√ø»’–¬‘ˆ»∑’Ô»À ˝∞¥»’∆⁄À≥–Ú≈≈¡–ππ≥… ˝¡–![]() £¨
£¨![]() µƒ«∞nœÓ∫ÕŒ™
µƒ«∞nœÓ∫ÕŒ™![]() £¨‘Úœ¬¡–Àµ∑®÷–’˝»∑µƒ «£® £©
£¨‘Úœ¬¡–Àµ∑®÷–’˝»∑µƒ «£® £©
A. ˝¡–![]() «µð‘ˆ ˝¡–B. ˝¡–
«µð‘ˆ ˝¡–B. ˝¡–![]() «µð‘ˆ ˝¡–
«µð‘ˆ ˝¡–
C. ˝¡–![]() µƒ◊Ó¥ÛœÓ «
µƒ◊Ó¥ÛœÓ «![]() D. ˝¡–
D. ˝¡–![]() µƒ◊Ó¥ÛœÓ «
µƒ◊Ó¥ÛœÓ «![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com