
【题目】已知A={x|x2≥9},B={x|﹣1<x≤7},C={x||x﹣2|<4}.
(1)求A∩B及A∪C;
(2)若U=R,求![]() .
.
【答案】(1) A∩B={x|3≤x≤7},A∪C={x|x≤﹣3或x>﹣2} (2) A∩U(B∩C)={x|x≥6或x≤﹣3}
【解析】试题分析:首先解不等式,化简集合A和C,再利用集合运算求出集合A与B的交集及集合A与C的并集;再求出集合B与C的交集,再求出B和C交集的补集,最后再求与集合A的交集.解题时注意集合的交、并、补的运算的定义,无限数集求交、并、补时,使用的工具是数轴.
试题解析:
(1)集合A中的不等式解得:x≥3或x≤﹣3,即A={x|x≥3或x≤﹣3};
集合C中的不等式解得:﹣2<x<6,即C={x|﹣2<x<6},
∴A∩B={x|3≤x≤7},A∪C={x|x≤﹣3或x>﹣2};
(2)∵B∩C={x|﹣1<x<6},全集U=R,
∴U(B∩C)={x|x≤﹣1或x≥6},
则A∩U(B∩C)={x|x≥6或x≤﹣3}


科目:高中数学 来源: 题型:
【题目】随着电子商务的发展,人们的购物习惯正在改变,基本上所有的需求都可以通过网络购物解决.小王是位网购达人,每次购买商品成功后都会对电商的商品和服务进行评价.现对其近年的200次成功交易进行评价统计,统计结果如下表所示.
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 80 | 40 | 120 |
对商品不满意 | 70 | 10 | 80 |
合计 | 150 | 50 | 200 |
(1)是否有![]() 的把握认为商品好评与服务好评有关? 请说明理由;
的把握认为商品好评与服务好评有关? 请说明理由;
(2)现从这200次交易中,按照“对商品好评”和“对商品不满意”采用分层抽样取出5次交易,然后从这5次交易中任选两次进行观察,求这两次交易中恰有一次“对商品好评”的概率.
附: (其中
(其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,则下列四个命题正确的是( )
的棱长为1,则下列四个命题正确的是( )
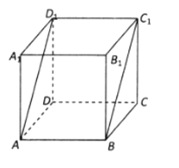
A.直线BC与平面![]() 所成的角等于
所成的角等于![]() B.点C到面
B.点C到面![]() 的距离为
的距离为![]()
C.两条异面直线![]() 和
和![]() 所成的角为
所成的角为![]() D.三棱柱
D.三棱柱![]() 外接球表面积为
外接球表面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B两点都在以PC为直径的球O的表面上,AB⊥BC,AB=2,BC=4,若球O的体积为![]() ,则三棱锥P-ABC表面积为___________.
,则三棱锥P-ABC表面积为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药公司研发一种新的保健产品,从生产的一批产品中抽取200盒作为样本,测量产品的一项质量指标值,该指标值越高越好.由测量结果得到如下频率分布直方图:
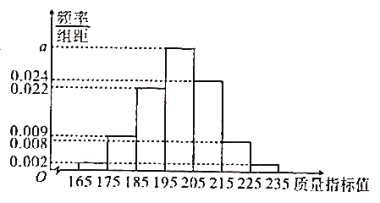
(Ⅰ)求![]() ,并试估计这200盒产品的该项指标的平均值;
,并试估计这200盒产品的该项指标的平均值;
(Ⅱ)国家有关部门规定每盒产品该项指标值不低于150均为合格,且按指标值的从低到高依次分为:合格、优良、优秀三个等级,其中![]() 为优良,不高于185为合格,不低于215为优秀.用样本的该项质量指标值的频率代替产品的该项质量指标值的概率.
为优良,不高于185为合格,不低于215为优秀.用样本的该项质量指标值的频率代替产品的该项质量指标值的概率.
①求产品该项指标值的优秀率;
②现从这批产品中随机抽取3盒,求其中至少有1盒该项质量指标值为优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() 得到如图所示的频率分布直方图.
得到如图所示的频率分布直方图.
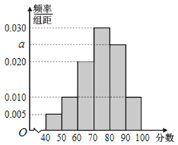
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请在答题卡上将![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
参考公式及数据: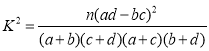 ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面使用类比推理,得到的结论正确的是( )
A. 直线![]() ,若
,若![]() ,则
,则![]() .类比推出:向量
.类比推出:向量![]() ,
,![]() ,
,![]() ,若
,若![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() .
.
B. 三角形的面积为![]() ,其中
,其中![]() ,
,![]() ,
,![]() 为三角形的边长,
为三角形的边长,![]() 为三角形内切圆的半径,类比推出,可得出四面体的体积为
为三角形内切圆的半径,类比推出,可得出四面体的体积为![]() ,(
,(![]() ,
,![]() ,
,![]() ,
,![]() 分别为四面体的四个面的面积,
分别为四面体的四个面的面积,![]() 为四面体内切球的半径)
为四面体内切球的半径)
C. 同一平面内,直线![]() ,若
,若![]() ,则
,则![]() .类比推出:空间中,直线
.类比推出:空间中,直线![]() ,若
,若![]() ,则
,则![]() .
.
D. 实数![]() ,若方程
,若方程![]() 有实数根,则
有实数根,则![]() .类比推出:复数
.类比推出:复数![]() ,若方程
,若方程![]() 有实数根,则
有实数根,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com