[题目]一个几何体的三视图如图所示.若该几何体的外接球表面积为.则该几何体的体积为( ) A. B. C. D. 题目和参考答案——青夏教育精英家教网—

【题目】一个几何体的三视图如图所示，若该几何体的外接球表面积为，则该几何体的体积为( )

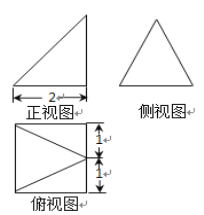
A. B. C. D.

【答案】B

【解析】

先将几何体还原得四棱锥P-ABCD，做底面中心的垂线，通过列方程找到球心的位置，进而再求四棱锥的高，从而可得体积.

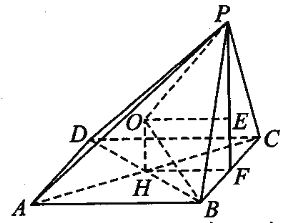
由三视图可知该几何体为四棱锥P-ABCD，其中ABCD是边长为2的正方形，侧面PBC垂直于底面ABCD，为等腰三角形.

设BC的中点为F，四边形ABCD的中心为点H，连接PF,FH，过点H作平面ABCD的垂线，则球心在该直线上，即为点O，过点O作于点E，连接OP.

设四棱锥P-ABCD的外接球半径为R，由其表面积为，得，解得.

设OH=x，则在直角三角形OHB中，有，解得.

在直角三角形POE中，，所以，解得.（负值已舍去）

所以PF=PE+EF=2.

所以四棱锥P-ABCD的体积.

故选B.

练习册系列答案

期末冲刺满分卷系列答案

相关习题

科目：高中数学 来源： 题型：

【题目】设椭圆：的离心率为，椭圆上一点到左右两个焦点、的距离之和是4.

（1）求椭圆的方程；

（2）已知过的直线与椭圆交于、两点，且两点与左右顶点不重合，若，求四边形面积的最大值.

科目：高中数学 来源： 题型：

【题目】甲、乙、丙三家企业产品的成本分别为10000，12000，15000，其成本构成如下图所示，则关于这三家企业下列说法错误的是（）

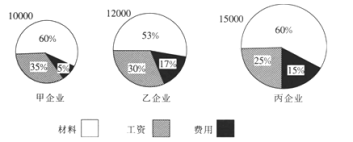
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业

C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业

科目：高中数学 来源： 题型：

【题目】（本小题满分12分）已知点为抛物线的焦点，点在抛物线上，且．

（Ⅰ）求抛物线的方程；

（Ⅱ）已知点，延长交抛物线于点，证明：以点为圆心且与直线相切的圆，必与直线相切．

科目：高中数学 来源： 题型：

【题目】2020年，我国继续实行个人所得税专项附加扣除办法，涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有人，现采用分层抽样的方法，从该单位上述员工中抽取50人调查专项附加扣除的享受情况.

（Ⅰ）应从老、中、青员工中分别抽取多少人？

（Ⅱ）抽取的50人中，享受至少两项专项附加扣除的员工有5人，分别记为.享受情况如下表，其中“○”表示享受，“×”表示不享受.现从这5人中随机抽取2人接受采访.