练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知等比数列{an}的各项均为正数，且log3a1+log3a2+log3a3+…+log3a10=10，则a5a6的值为（　　）
    A．3B．6C．9D．18

    分析 利用等比数列的性质、对数函数性质、运算法则求解．

    解答 解：∵等比数列{an}的各项均为正数，且log3a1+log3a2+log3a3+…+log3a10=10，
    ∴log3（a1a2a3a4a5a6a7a8a9a10）=$lo{g}_{3}（{a}_{5}{a}_{6}）^{5}$=10，
    ∴a5a6=9．
    故选：C．

    点评 本题考查等比数列两项积的求法，是基础题，解题时要认真审题，注意等比数列的性质、对数函数性质、运算法则的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．在正方体ABCD-A1B1C1D1中，E、F分别是BB1、CD的中点
    （1）求AE与D1F所成的角
    （文科）（2）证明：AD⊥D1F；
    （理科）（2）证明：面AED⊥面A1FD1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知A（0，1），B（0，-1），点P满足$\frac{\sqrt{{x}^{2}+（y-1）^{2}}}{|y-\frac{1}{4}|}$=2，则|PA|-|PB|等于（　　）
    A．1B．-1C．±1D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．在等腰直角三角形ABC中，AC=BC=1，点M，N分别为AB，BC的中点，点P为△ABC内部任一点，则$\overrightarrow{AN}•\overrightarrow{MP}$取值范围为（　　）
    A．$（{-\frac{3}{4}，\frac{3}{4}}）$B．$（{-\frac{4}{3}，\frac{4}{3}}）$C．$（{0，\frac{3}{4}}）$D．$（{-\frac{3}{4}，0}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

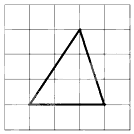
    11．网格纸的小正方形边长为1，一个正三棱锥的左视图如图所示，则这个正三棱锥的体积为（　　）
    A．$\sqrt{3}$B．$3\sqrt{3}$C．$\frac{9}{2}$D．$\frac{9}{2}\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

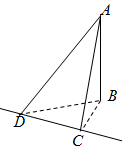    1．要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD=120°，CD=60m，则电视塔的高度为（　　）
    A．60mB．40mC．$30\sqrt{3}m$D．30m

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知递增的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2和a4的等差中项．
    （ I）求数列{an}的通项公式an；
    （Ⅱ）令${b_n}={a_n}•{log_{\frac{1}{2}}}{a_n}$，Sn=b1+b2+…bn，求Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．为了考查培育的某种植物的生长情况，从试验田中随机抽取100柱该植物进行检测，得到该植物高度的频数分布表如下：
    组序高度区间频数频率
    　1[230，235）140.14
    2[235，240）①0.26
    3[240，245）②0.20
    4[245，250）30③
    5[250，255）10④
    合计1001.00
    （Ⅰ）写出表中①②③④处的数据；
    （Ⅱ）用分层抽样法从第3、4、5组中抽取一个容量为6的样本，则各组应分别抽取多少个个体？
    （Ⅲ）在（Ⅱ）的前提下，从抽出的容量为6的样本中随机选取两个个体进行进一步分析，求这两个个体中至少有一个来自第3组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．当函数y=sinx-$\sqrt{3}$cosx（0≤x＜2π）取得最大值时，x=（　　）
    A．$\frac{π}{2}$B．$\frac{5π}{6}$C．$\frac{7π}{6}$D．$\frac{3π}{2}$

    查看答案和解析>>

    同步练习册答案