
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]()
![]() ,使得
,使得![]() 函数满足:(1)
函数满足:(1)![]() 在
在![]() 上是单调函数;(2)
上是单调函数;(2)![]() 在
在![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数![]() 的“和谐区间”,下列结论错误的是( )
的“和谐区间”,下列结论错误的是( )
A.函数![]() 存在“和谐区间”
存在“和谐区间”
B.函数![]() 不存在“和谐区间”
不存在“和谐区间”
C.函数![]()
![]() 存在“和谐区间”
存在“和谐区间”
D.函数![]() (
(![]() ,
,![]() )不存在“和谐区间”
)不存在“和谐区间”
【答案】D
【解析】
试题分析:函数中存在“和谐区间”,则①![]() 在
在![]() 内是单调函数;②
内是单调函数;②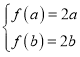 或
或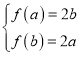 ,若
,若![]() ,若存在“和谐区间”
,若存在“和谐区间”![]() ,则此时函数单调递增,则由
,则此时函数单调递增,则由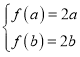 ,得
,得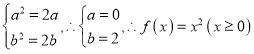 存在“和谐区间”
存在“和谐区间”![]() 正确.若
正确.若![]() ,若存在“和谐区间”
,若存在“和谐区间”![]() ,则此时函数单调递增, 则由
,则此时函数单调递增, 则由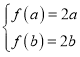 ,得
,得 ,即
,即![]() 是方程
是方程![]() 的两个不等的实根, 构建函数
的两个不等的实根, 构建函数![]() ,所以函数在
,所以函数在![]() 上单调减,在
上单调减,在![]() 上单调增,
上单调增,![]() 函数在
函数在![]() 处取得极小值,且为最小值,
处取得极小值,且为最小值,![]() ,无解,故函数不存在“和谐区间”,
,无解,故函数不存在“和谐区间”,![]() 正确.若函数
正确.若函数![]() ,
,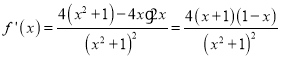 ,若存在“和谐区间”
,若存在“和谐区间”![]() ,则由
,则由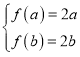 ,得
,得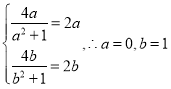 ,即存在“和谐区间”
,即存在“和谐区间”![]() ,
,![]() 正确.若函数
正确.若函数![]() ,不妨设
,不妨设![]() ,则函数定义域内为单调增函数,若存在“和谐区间”
,则函数定义域内为单调增函数,若存在“和谐区间”![]() , 则由
, 则由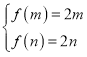 ,得
,得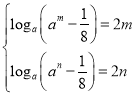 ,即
,即![]() 是方程
是方程![]() 的两个根,即
的两个根,即![]() 是方程
是方程![]() 的两个根,由于该方程有两个不等的正根,故存在“和谐区间”
的两个根,由于该方程有两个不等的正根,故存在“和谐区间”![]() ,
,![]() 结论错误,故选D.
结论错误,故选D.


科目:高中数学 来源: 题型:
【题目】无穷数列![]()
![]() ,若存在正整数
,若存在正整数![]() ,使得该数列由
,使得该数列由![]() 个互不相同的实数组成,且对于任意的正整数
个互不相同的实数组成,且对于任意的正整数![]() ,
,![]() 中至少有一个等于
中至少有一个等于![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .集合
.集合![]() .
.
(1)若![]() ,
,![]() ,判断数列
,判断数列![]() 是否具有性质
是否具有性质![]() ;
;
(2)数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)数列![]() 具有性质
具有性质![]() ,对于
,对于![]() 中的任意元素
中的任意元素![]() ,
,![]() 为第
为第![]() 个满足
个满足![]() 的项,记
的项,记![]()
![]() ,证明:“数列
,证明:“数列![]() 具有性质
具有性质![]() ”的充要条件为“数列
”的充要条件为“数列![]() 是周期为
是周期为![]() 的周期数列,且每个周期均包含
的周期数列,且每个周期均包含![]() 个不同实数”.
个不同实数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数![]() 是奇函数
是奇函数
(1)求![]() 、
、![]() 的值;
的值;
(2)判断![]() 的单调性(不需要证明),并写出
的单调性(不需要证明),并写出![]() 的值域;
的值域;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国际田联的标准400米跑道,它的最内侧跑道的边线是由两根84.39米的平行直线和两段半径36.80米的半圆组成,每根跑道宽1.22米(道与道间的划线宽度忽略不计).比赛时运动员从下方标有数字处出发.为了比賽公平,外道的运动员的起跑点较内道的会有一定的提前量,使得所有运动员跑过的路程完全一致.假设每位运动员都会沿着自己道次的最内侧跑.

(1)试给出400米比赛各道次提前量![]() 关于道次
关于道次![]() 之间的函数关系,并完成下表(精确到0.01米)
之间的函数关系,并完成下表(精确到0.01米)
(2)800米比赛的规则是从出发处按道次跑完第一个弯道后可以开始并道赛跑,请你设计第8道选手的最优跑步路线并给出他起跑的提前量应该是多少.
道次 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
提前量(米) | 7.67 | 15.33 | 23.00 | 30.66 | 38.33 | 46.00 | 53.66 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于往届高三年级数学学科的学习方式大都是“刷题一讲题一再刷题”的模式,效果不理想,某市一中的数学课堂教改采用了“记题型一刷题一检测效果”的模式,并记录了某学生的记题型时间![]() (单位:
(单位:![]() )与检测效果
)与检测效果![]() 的数据如下表所示.
的数据如下表所示.
记题型时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
检测效果 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系,请用相关系数
之间具有线性相关关系,请用相关系数![]() 加以说明(若
加以说明(若![]() ,则认为
,则认为![]() 与
与![]() 有很强的线性相关关系,否则认为没有很强的线性相关关系);
有很强的线性相关关系,否则认为没有很强的线性相关关系);
(2)建立![]() 关于
关于![]() 的回归方程,并预测该学生记题型
的回归方程,并预测该学生记题型的检测效果;
(3)在该学生检测效果不低于3.6的数据中任取2个,求检测效果均高于4.4的概率.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)判断并证明![]() 的单调性;
的单调性;
(Ⅱ)是否存在实数![]() ,使函数
,使函数![]() 为奇函数?证明你的结论;
为奇函数?证明你的结论;
(Ⅲ)在(Ⅱ)的条件下,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,
中,![]() ,
,![]() .前
.前![]() 项和
项和![]() 满足
满足![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)求证:数列![]() 是等比数列;
是等比数列;
(3)若![]() ,现按如下方法构造项数为
,现按如下方法构造项数为![]() 的有穷数列
的有穷数列![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .记数列
.记数列![]() 的前
的前![]() 项和
项和![]() ,试问:
,试问:![]() 是否能取整数?若能,请求出
是否能取整数?若能,请求出![]() 的取值集合:若不能,请说明理由.
的取值集合:若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖北省2019年新高考方案公布,实行“![]() ”模式,即“3”是指语文、数学、外语必考,“1”是指物理、历史两科中选考一门,“2”是指生物、化学、地理、政治四科中选考两门,在所有选科组合中某学生选择考历史和化学的概率为( )
”模式,即“3”是指语文、数学、外语必考,“1”是指物理、历史两科中选考一门,“2”是指生物、化学、地理、政治四科中选考两门,在所有选科组合中某学生选择考历史和化学的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com